Tìm các số nguyên x,y,z biết
a,
5.(x+y+z)=z.y.z
b,x2+y2+z2=x.y.z
Tìm các số nguyên a,v,c,d,e,biết tổng của chúng bằng 0 và a+b=c+d=d+e=2
Tìm các số nguyên x,y,z biết x+y+z=0;x+y=3;y+z=-1
tìm các số nguyên x biết x + y = 2 ; y + z =3 ; z + x = -5
ta có x + y = 2 suy ra x= 2 - y
z + x = -5 suy ra x= -5-z
suy ra x=2 -y = -5 -z=-5-z-2+y= -7 - z + y
thay x=-7 - z + y vào z + x = -5 ta được
z - 7 -z +y = - 5
-7 + y = -5
y=2
suy ra x= -2 , z=-3
tìm các số nguyên x biết x + y = 2 ; y + z =3 ; z + x = -5
Giải:
Ta có:
x + y = 2
y + z = 3
z + x = -5
\(\Rightarrow x+y+y+z+z+x=2+3+\left(-5\right)\)
\(\Rightarrow2x+2y+2x=0\)
\(\Rightarrow2\left(x+y+z\right)=0\)
\(\Rightarrow x+y+z=0\)
\(\Rightarrow x=0-3=-3\)
\(\Rightarrow y=0-\left(-5\right)=5\)
\(\Rightarrow z=0-2=-2\)
Vậy bộ số \(\left(x;y;z\right)\) là \(\left(-3;5;-2\right)\)
ta có x + y = 2, y + z = 3, z + x = -5
=> x + y + y +z + z + x = 2 + 3 + -5
=> 2(x + y+ z) = 0
=>x + y + z = 0
mà x + y = 2 => z= -2
tương tự => x = -3 và y = 5
Tìm các số a, b, c biết 2a = 3b, 5b = 7c và 3a – 7b + 5c = -
30.
Tìm các số x, y, z biết x : y : z = 3 : 4 : 5 và 2𝑥^2 + 2𝑦^2 -
3𝑧^2 = -100.
\(2a=3b\Rightarrow\dfrac{a}{3}=\dfrac{b}{2}\Rightarrow\dfrac{a}{21}=\dfrac{b}{14}\\ 5b=7c\Rightarrow\dfrac{b}{7}=\dfrac{c}{5}\Rightarrow\dfrac{b}{14}=\dfrac{c}{10}\\ \Rightarrow\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{21}=\dfrac{b}{14}=\dfrac{c}{10}=\dfrac{3a}{63}=\dfrac{7b}{98}=\dfrac{5c}{50}=\dfrac{3a-7b+5c}{63-98+50}=\dfrac{-30}{15}=-2\\ \Rightarrow\left\{{}\begin{matrix}a=-42\\b=-28\\c=-20\end{matrix}\right.\)
\(x:y:z=3:4:5\Rightarrow\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\Rightarrow x=3k;y=4k;z=5k\)
\(2x^2+2y^2-3z^2=-100\\ \Rightarrow18k^2+32k^2-75k^2=-100\\ \Rightarrow-25k^2=-100\Rightarrow k^2=4\Rightarrow\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=8;z=10\\x=-6;y=-8;z=-10\end{matrix}\right.\)
\(2a=3b\text{⇒}a=\dfrac{3b}{2}\) , \(5b=7c\text{⇒}c=\dfrac{5c}{7}\)
\(3a-7b+5c\) \(=-30\)
⇔ \(3.\dfrac{3b}{2}-7b+5.\dfrac{5b}{7}=-30\)
⇔\(63b-98b+50b=-420\)
⇔\(b=-28\) ⇒\(\left\{{}\begin{matrix}a=-42\\c=-20\end{matrix}\right.\)
Cho các số thực dương x,y,z thỏa mãn: x2+y2+z2=3. Chứng minh rằng:x3+y3+z3+x+y+z ≥ 6
\(x^3+x\ge2\sqrt{x^4}=2x^2\)
Tương tự:
\(y^3+y\ge2y^2\)
\(z^3+z\ge2z^2\)
Cộng vế:
\(x^3+y^3+z^3+x+y+z\ge2\left(x^2+y^2+z^2\right)=6\)
Dấu "=" xảy ra khi \(x=y=z=1\)
Tìm các số hữu tỉ x, y, z biết rằng: x(x + y + z) = -5; y(x + y + z) = 9; z(x + y + z) = 5.
Cộng theo từng vế các đẳng thức đã cho, ta được:
x.(x + y + z) + y(x + y + z) + z.(x+ y + z) = - 5 + 9 + 5
⇔ (x + y + z). (x + y + z ) = 9
Suy ra: (x + y + z)2 = 9 ⇒ x + y + z = ±3
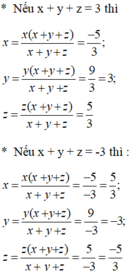
Tìm các số hữu tỉ x, y, z biết rằng : x(x + y + z) = - 5 ; y( x + y + z) = 9 ; z(x + y + z) = 5
với x,y,z thuộc số hữu tì ta có
bn tự chép đề tại chỗ này nh a.
từ đề bài ,cộng vế theo vế ta có
x(x+y+z)+y(x+y+z)+z(x+y+z)=-5+9+5=9
suy ra (x+y+z)(x+y+z)=9 suy ra (x+y+z)^2=3^2 hay =(-3)^2
suy ra x+y+z=3 hay=-3
xét trường hợp 1 ta có x+y+z=3
suy ra x(x+y+z)=-5 suy ra x=-5/3
suy ra y=9/3=3
suy ra z=5/3
tương tự xét trường hợp thứ hai ta có x+y+z=-3
suy ra x=-5/-5=5/3
suy ra y=9/-3=-3
suy ra z=5/-3=-5/3
Tìm các số hữu tỉ x, y, z biết rằng:
x(x + y + z) = -5; y(x + y + z) = 9; z(x + y + z) = 5.
bạn tham khảo nè:
với x,y,z thuộc số hữu tì ta có
bn tự chép đề tại chỗ này nh a.
từ đề bài ,cộng vế theo vế ta có
x(x+y+z)+y(x+y+z)+z(x+y+z)=-5+9+5=9
suy ra (x+y+z)(x+y+z)=9 suy ra (x+y+z)^2=3^2 hay =(-3)^2
suy ra x+y+z=3 hay=-3
xét trường hợp 1 ta có x+y+z=3
suy ra x(x+y+z)=-5 suy ra x=-5/3
suy ra y=9/3=3
suy ra z=5/3
tương tự xét trường hợp thứ hai ta có x+y+z=-3
suy ra x=-5/-5=5/3
suy ra y=9/-3=-3
suy ra z=5/-3=-5/3
Cộng theo từng vế các đẳng thức đã cho, ta được:
\(\left(x+y+z\right)^2=9\Rightarrow x+y+z=\pm3\)
Nếu \(x+y+z=3\)thì \(x=\frac{-5}{3};y=3;z=\frac{5}{3}\)
Nếu \(x+y+z=-3\)thì \(x=\frac{5}{3};y=-3;z=\frac{-5}{3}\)
c) C = x(y2 +z2)+y(z2 +x2)+z(x2 +y2)+2xyz.
d) D = x3(y−z)+y3(z−x)+z3(x−y).
e) E = (x+y)(x2 −y2)+(y+z)(y2 −z2)+(z+x)(z2 −x2).
b) x2 +2x−24 = 0.
d) 3x(x+4)−x2 −4x = 0.
f) (x−1)(x−3)(x+5)(x+7)−297 = 0.
(2x−1)2 −(x+3)2 = 0.
c) x3 −x2 +x+3 = 0.
e) (x2 +x+1)(x2 +x)−2 = 0.
a) A = x2(y−2z)+y2(z−x)+2z2(x−y)+xyz.
b) B = x(y3 +z3)+y(z3 +x3)+z(x3 +y3)+xyz(x+y+z). c) C = x(y2 −z2)−y(z2 −x2)+z(x2 −y2).
Đề bài yêu cầu gì vậy em.