-Tìm một cách chứng minh khác của bất đẳng thức tam giác
Lấy bài nhanh nha
a, Tìm một cách chứng minh khác của bất đẳng thức tam giác
b, Cho tam giác MNP. Gọi I là trung điểm của đoạn thẳng MN. Chứng minh rằng : PM + PN > 2 PI
a, Tìm một cách chứng minh khác của bất đẳng thức tam giác
b, Cho tam giác MNP. Gọi I là trung điểm của đoạn thẳng MN. Chứng minh rằng : PM + PN > 2 PI
a, Tìm một cách chứng minh khác của bất đẳng thức tam giác
b, Cho tam giác MNP. Gọi I là trung điểm của đoạn thẳng MN. Chứng minh rằng : PM + PN > 2 PI
Câu 2:
a) Tìm một cách chứng minh khác của bất đẳng thức tam giác.
b) Cho tam giác MNP. Gọi I là trung điểm của đoạn thẳng MN. Chứng minh rằng: PM + PN > 2 PI.
Giúp mk mấy bn
a) Tìm một cách chứng minh khác của bất đẳng thức tam giác.
b) Cho tam giác MNP. Gọi I là trung điểm của đoạn thẳng MN. Chứng minh rằng: PM + PN > 2 PI.
Mọi người ơi giúp mik vs đg cần gấp
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).
Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại.
Xét tam giác ABC vì BC là cạnh lớn nhất nên AB < BC và AC < BC.
Mà ta lại có: AC > 0 và AB > 0 hay 0 < AC và 0 < AB
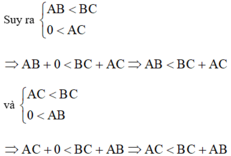
⇒ Đpcm
Một cách chứng minh khác của bất đẳng thức tam giác:
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).
Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở Bài 1 để chứng minh AB + AC > BC.
Theo giả thiết, tam giác ABC có độ dài cạnh BC là lớn nhất nên chân đường vuông góc kẻ từ A đến cạnh BC chắn chắn phải nằm giữa B và C.
Suy ra H nằm giữa B và C.
⇒ HB + HC = BC
+) Xét tam giác AHB vuông tại H ta có: HB < AB (1) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
+) Xét tam giác AHC vuông tại H ta có: HC < AC (2) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
Lấy (1) + (2) ta được:
HB + HC < AB + AC
Mà HB + HC = BC suy ra BC < AB + AC hay AB + AC > BC
Một cách chứng minh khác của bất đẳng thức tam giác :
Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC \(\left(H\in BC\right)\)
a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở bài 1 để chứng minh AB + AC > BC
b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại
a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
a) Tìm 1 cách chứng minh khác của bất đẳng thức tam giác
b) Cho tam giác MNP . Gọi I là trung điểm của đoạn thằng MN . CMR : PM+PN>2PI
a) Hình mình vẽ hơi xấu nha
Kẻ đg AH vuông góc vs BC (H thuộc BC)
Có tg ABH vuông tại H, nên AB> BH(1)
Có tg AHC vuông tại H, nên AC> HC (2)
Mà BC = BH+ HC (3) Từ (1), (2), (3) suy ra :
BC< AB+ AC
2 cái còn lại giải tương tự nhan! Tại mk đang bận nên kh giải hết 3 cái đc. Thông cảm nhé!