Giải các bất phương trình lôgarit:
a) log12(8- 6x) ≥ 6;
c) log0,4x – log9(x- 4) < log0,43;
Những câu hỏi liên quan
Giải bất phương trình
log
1
2
(
2
x
+
3
)
log
1
2
(
3
x
+
1
)
A.
-
1
3
x
2
B.
-
1...
Đọc tiếp
Giải bất phương trình log 1 2 ( 2 x + 3 ) > log 1 2 ( 3 x + 1 )
A. - 1 3 < x < 2
B. - 1 3 < x < 5
C. x > 5
D. x > 2
Giải bất phương trình:
\(log12(2x+3)>log12(3x+1)(1)log12(2x+3)>log12(3x+1)(1) \)
Giải bất phương trình
log
1
2
(
x
−
1
)
2
. A.
1
x
5
4
B.
x
5
4
C. x 1 D.
x
5
4
Đọc tiếp
Giải bất phương trình log 1 2 ( x − 1 ) > 2 .
A. 1 < x < 5 4
B. x > 5 4
C. x > 1
D. x < 5 4
Giải bất phương trình
l
o
g
1
2
[
l
o
g
3
(
x
+
1
)
]
0
A
.
x
-
1
B
.
0
x
2
C
.
...
Đọc tiếp
Giải bất phương trình l o g 1 2 [ l o g 3 ( x + 1 ) ] < 0
A . x > - 1
B . 0 < x < 2
C . - 1 < x < 2
D . x > 2
Giải bất phương trình
log
1
2
(
x
2
-
3
x
+
2
)
≥
-
1
A. B. C. D.
Đọc tiếp
Giải bất phương trình log 1 2 ( x 2 - 3 x + 2 ) ≥ - 1
A. 
B. 
C.
D.
Giải bất phương trình
log
1
2
(
log
3
(
2
x
-
1
)
)
1000
0
A.
1
2
x
2
v
à
...
Đọc tiếp
Giải bất phương trình log 1 2 ( log 3 ( 2 x - 1 ) ) 1000 > 0
A. 1 2 < x < 2 v à x ≠ 1
B. 2 3 < x < 2 v à x ≠ 1
C. 1 <x <2
D. 1 < x < 3
Tìm tập nghiệm của bất phương trình:
log
1
2
(
x
2
+
2
x
−
8
)
≥
−
4
A. (-4; 2) B. [-6; 4) C.
[
−
6
;
−
4
]
∪
[
2
;
4
]...
Đọc tiếp
Tìm tập nghiệm của bất phương trình:
log 1 2 ( x 2 + 2 x − 8 ) ≥ − 4
A. (-4; 2)
B. [-6; 4)
C. [ − 6 ; − 4 ] ∪ [ 2 ; 4 ]
D. [ − 6 ; − 4 ) ∪ ( 2 ; 4 ]
Số nghiệm nguyên của bất phương trình
log
1
2
(
x
2
+
2
x
-
8
)
≥
-
4
là A. Vô số B. 2 C. 4 D. 6
Đọc tiếp
Số nghiệm nguyên của bất phương trình
log 1 2 ( x 2 + 2 x - 8 ) ≥ - 4 là
A. Vô số
B. 2
C. 4
D. 6
Chọn B.
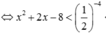
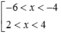
Vậy bất phương trình có 2 nghiệm nguyên.
Đúng 0
Bình luận (0)
Nghiệm của bất phương trình
log
1
2
(
2
x
+
3
)
log
1
2
(
3
x
+
1
)
là
Đọc tiếp
Nghiệm của bất phương trình log 1 2 ( 2 x + 3 ) > log 1 2 ( 3 x + 1 ) là
