GIÚP EM VỚI MNG ƠI

Giúp tớ trước 10h tối nay với ạ!! Cảm ơn mng nhiều!! Mng ơi giúp em với ạaa
Câu 2:
uses crt;
var a:array[1..100]of integer;
i,n,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
if (4<a[i]) and (a[i]<15) then t:=t+a[i];
writeln(t);
readln;
end.
GIÚP EM VỚI MNG ƠI
Mng ơi giúp em với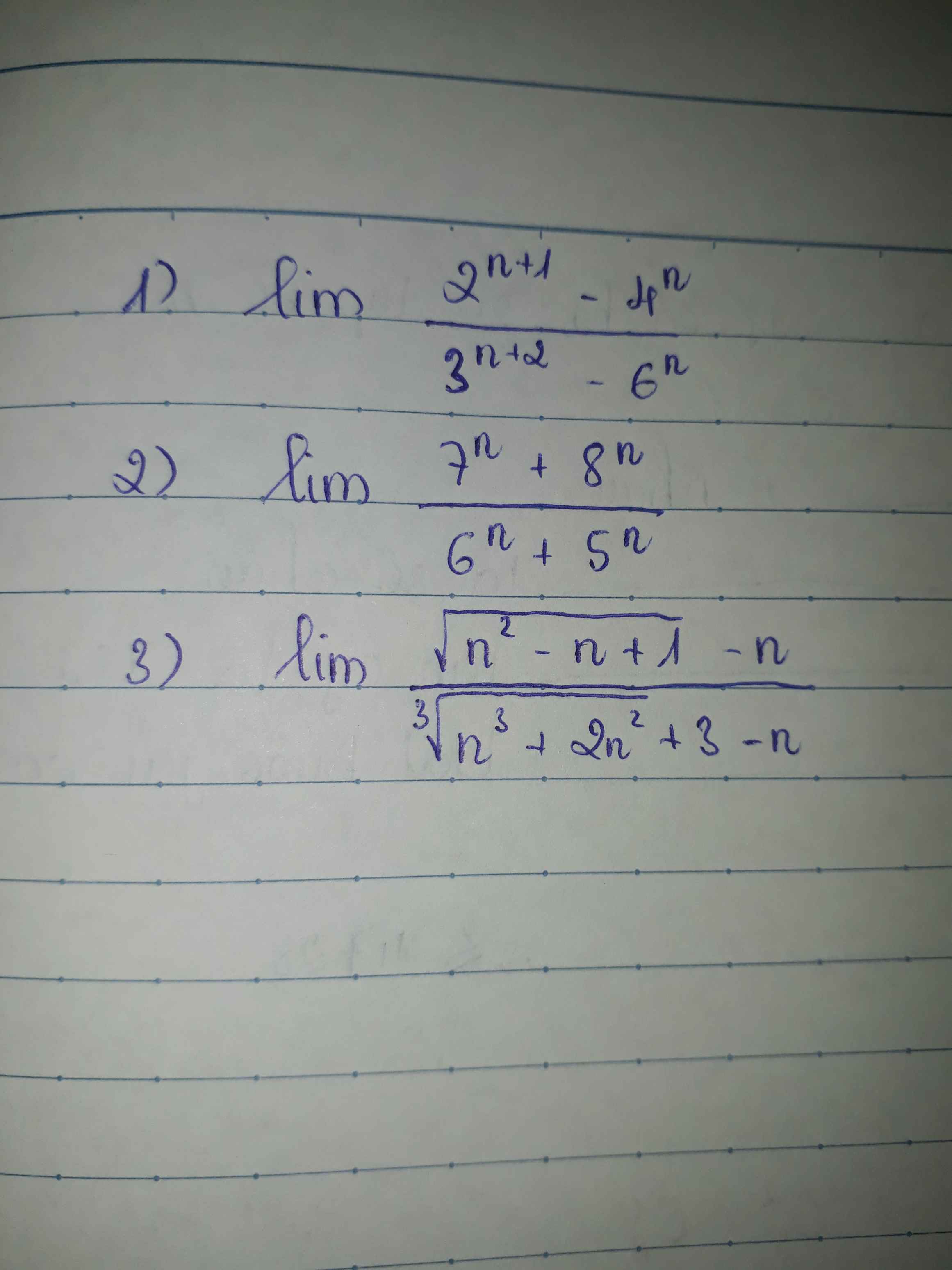
\(\lim\dfrac{2^{n+1}-4^n}{3^{n+2}-6^n}=\lim\dfrac{2.2^n-4^n}{9.3^n-6^n}=\lim\dfrac{2\left(\dfrac{2}{6}\right)^n-\left(\dfrac{4}{6}\right)^n}{9\left(\dfrac{3}{6}\right)^n-1}=\dfrac{2.0-0}{9.0-1}=0\)
\(\lim\dfrac{7^n+8^n}{6^n+5^n}=\lim\dfrac{\left(\dfrac{7}{8}\right)^n+1}{\left(\dfrac{6}{8}\right)^n+\left(\dfrac{5}{8}\right)^n}=\dfrac{0+1}{0+0}=\dfrac{1}{0}=+\infty\)
Câu 3 là con số 3 dưới mẫu ở trong hay ngoài căn vậy nhỉ?
\(\lim\dfrac{\sqrt[]{n^2-n+1}-n}{\sqrt[3]{n^3+2n^2+3}-n}\)
\(=\lim\dfrac{\left(\sqrt[]{n^2-n+1}-n\right)\left(\sqrt[]{n^2-n+1}+n\right)\left(\sqrt[3]{\left(n^3+2n^2+3\right)^2}+n\sqrt[3]{n^3+2n^2+3}+n^2\right)}{\left(\sqrt[3]{n^3+2n^2+3}-n\right)\left(\sqrt[3]{\left(n^3+2n^2+3\right)^2}+n\sqrt[3]{n^3+2n^2+3}+n^2\right)\left(\sqrt[]{n^2-n+1}+n\right)}\)
\(=\lim\dfrac{\left(-n+1\right)\left(\sqrt[3]{\left(n^3+2n^2+3\right)^2}+n\sqrt[3]{n^3+2n^2+3}+n^2\right)}{\left(2n^2+3\right)\left(\sqrt[]{n^2-n+1}+n\right)}\)
\(=\lim\dfrac{\left(-1+\dfrac{1}{n}\right)\left(\sqrt[3]{\left(1+\dfrac{2}{n}+\dfrac{3}{n^3}\right)^2}+\sqrt[3]{1+\dfrac{2}{n}+\dfrac{3}{n^3}}+1\right)}{\left(2+\dfrac{3}{n^2}\right)\left(\sqrt[]{1-\dfrac{1}{n}+\dfrac{1}{n^2}}+1\right)}\)
\(=\dfrac{-1.\left(1+1+1\right)}{2.\left(1+1\right)}=-\dfrac{3}{4}\)
Giúp em câu 7 với mng ơi
7)
\(=\dfrac{\left(5-\sqrt{5}\right).\left(1+\sqrt{5}\right)}{\left(1-\sqrt{5}\right)\left(1+\sqrt{5}\right)}+\dfrac{3\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}+\sqrt{5}\right)}\)
\(=\dfrac{\left(5-\sqrt{5}\right)\left(1+\sqrt{5}\right)}{1-5}+\dfrac{3\left(\sqrt{2}+\sqrt{5}\right)}{4-5}\)
\(=\dfrac{5+5\sqrt{5}-\sqrt{5}-5}{4}+3\left(\sqrt{2}+\sqrt{5}\right)\)
=\(\dfrac{4\sqrt{5}}{4}+3\left(\sqrt{2}+\sqrt{5}\right)\)
\(=\sqrt{5}+3\sqrt{2}+3\sqrt{5}\)
\(=4\sqrt{5}+3\sqrt{2}\)
7: Ta có: \(\dfrac{5-\sqrt{5}}{1-\sqrt{5}}+\dfrac{3}{\sqrt{2}-\sqrt{5}}\)
\(=-\sqrt{5}-3\left(\sqrt{5}+\sqrt{2}\right)\)
\(=-\sqrt{5}-3\sqrt{5}-3\sqrt{2}\)
\(=-4\sqrt{5}-3\sqrt{2}\)
Mng ơi giúp em gấp với ạ 
 mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
mng ơi giúp em với ạ! e đag cần gấp! e cảm ơn mng nhiều lắmm <33
Bài 5:
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y-z}{2+3-4}=\dfrac{-20}{1}=-20\)
Do đó: x=-40; y=-60; z=-80
Mng ơi giúp em với LÀM LÁ THƯ DỰA VÀO CÁC GỢI Ý Ở DƯỚI(suggested work ) em đa tạ mng 😭
CÂU 10 MNG ƠI GIÚP EM VỚI Ạ

Mng ơi giúp em với ạ. Câu nào em khoanh bằng mực màu đỏ thì mọi người giải dùm em. Câu mà đã bôi màu vàng là em đã làm thì mng xem xem có đúng không thì mng sửa dùm với ạ!!
1. should ask
*must not ask là sai vì người quản lí mới nên hỏi vài câu hỏi trước khi thực hiện thay đổi
*have to ask (mang tính chủ quan) nên có làm hay không làm cũng được nên ta không chọn đáp án này
2. could prevent
Vì sau would, could là V_inf