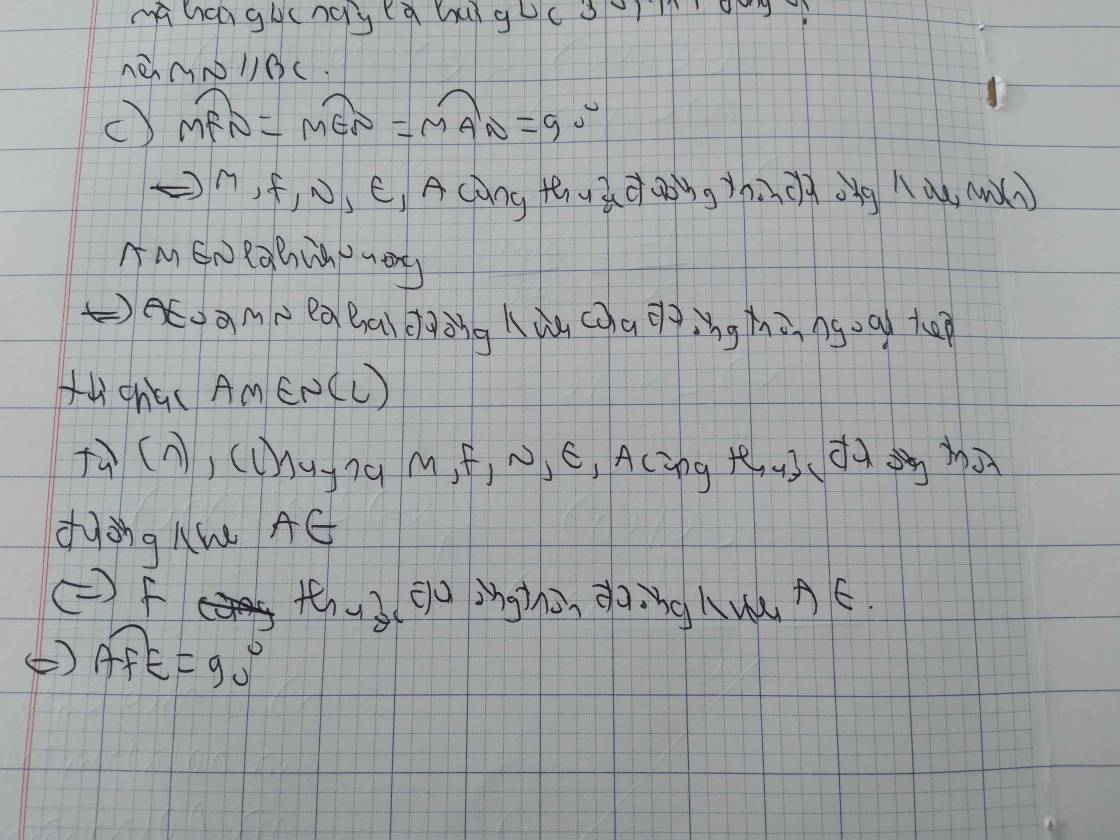Cầu 12 Cho tam giác ABC vuông tại A. Gọi N là
trung diểm của BC,
qua N kẻ các đường thắng
vuông góc với AB tại E và đuờng thắng vuông góc với AC
tại D.
a) Chứng minh tứ giác AEND là hinh chữ nhật.
b) Già sử AB -Scm và AC-8cm. Tinh diện tich tam
giác ABC.
c) Tam giác vuông ABC phải có thêm điều
kiện gì thì từ giác AEND
là hình vuông? di Goi
M đối ximg với N qua D, K là giao diểm của
BD và MC. Chứmg
minh KC- 2KM.

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB6m;AC8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 24HE mũ 2+4HD mũ 2
Đọc tiếp
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
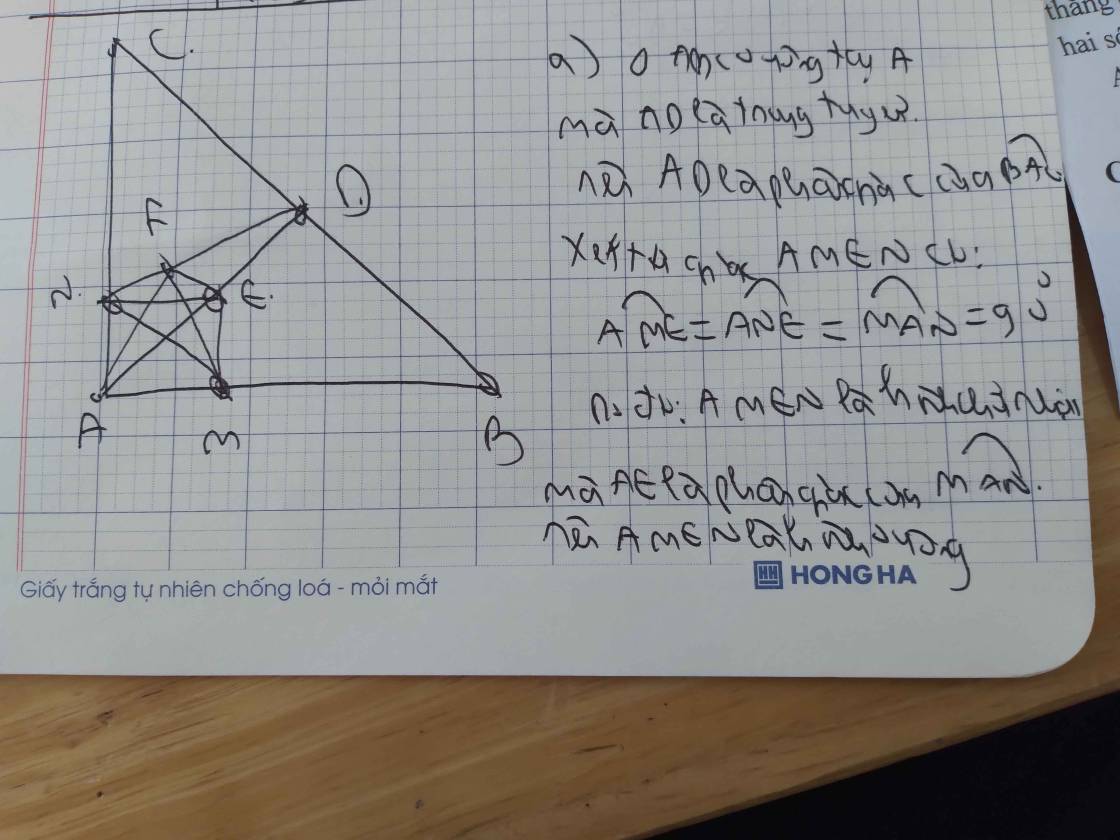
Bài 4. Cho tam giác ABC vuông cân tại A. Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì (E khác A và D). Qua E kẻ các đường vuông góc với AB, AC lần lượt tại M và N. a) Chứng minh tứ giác AMEN là hình vuông. b) Chứng minh MN // BC. ...
Đọc tiếp
Bài 4. Cho tam giác ABC vuông cân tại A. Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì (E khác A và D). Qua E kẻ các đường vuông góc với AB, AC lần lượt tại M và N. a) Chứng minh tứ giác AMEN là hình vuông. b) Chứng minh MN // BC. c) Qua M kẻ đường thẳng vuông góc với DN tại F. Chứng minh AFE 90 độ d) Chứng minh B, E, F thẳng hàng.
a: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là tia phân giác của \(\widehat{BAC}\) và AD\(\perp\)BC
Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
Do đó: AMEN là hình chữ nhật
Hình chữ nhật AMEN có AE là phân giác của \(\widehat{MAN}\)
nên AMEN là hình vuông
b: AMEN là hình vuông
=>\(\widehat{AMN}=45^0\)
=>\(\widehat{AMN}=\widehat{ABC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên MN//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB>AC). Kẻ đường cao AH (H thuộc BC). Gọi D là trung điểm của AB. Qua A kẻ đường thẳng vuông góc với CD cắt CD và CB lần lượt tại E và F. Gọi K là hình chiếu vuông góc của D trên BC.
1) Chứng minh rằng các tam giác ADE và CDA đồng dạng với nhau.
2) Chứng minh rằng BD.BC = BE.CD.
Cho tam giác ABC vuông cân tại A . Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E khác A và D ). Qua E kẻ các đường vuông góc với AB AC , lần lượt tại M N, .
a) Chứng minh tứ giác AMEN là hình vuông.
b) Chứng minh MN BC / / .
c) Qua M kẻ đường thẳng vuông góc với DN tại F . Chứng minh AFE = 90 . d) Chứng minh B E F , , thẳng hàng.
Cho tam giác ABC vuông cân tại A . Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E khác A và D ). Qua E kẻ các đường vuông góc với AB AC , lần lượt tại M N, .
a) Chứng minh tứ giác AMEN là hình vuông.
b) Chứng minh MN BC / / .
c) Qua M kẻ đường thẳng vuông góc với DN tại F . Chứng minh AFE = 90 . d) Chứng minh B E F , , thẳng hàng.
a: Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{NAM}=90^0\)
Do đó: AMEN là hình chữ nhật
mà AE là tia phân giác
nen AMEN là hình vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A . Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E khác A và D ). Qua E kẻ các đường vuông góc với AB AC , lần lượt tại M N, .
a) Chứng minh tứ giác AMEN là hình vuông.
b) Chứng minh MN BC / / .
c) Qua M kẻ đường thẳng vuông góc với DN tại F . Chứng minh AFE = 90 . d) Chứng minh B E F , , thẳng hàng.
Cho tam giác ABC vuông cân tại A . Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E khác A và D ). Qua E kẻ các đường vuông góc với AB AC , lần lượt tại M N, .
a) Chứng minh tứ giác AMEN là hình vuông.
b) Chứng minh MN BC / / .
c) Qua M kẻ đường thẳng vuông góc với DN tại F . Chứng minh AFE = 90 . d) Chứng minh B E F , , thẳng hàng.
a: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là tia phân giác của \(\widehat{BAC}\)
Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
=>AMEN là hình chữ nhật
Hình chữ nhật AMEN có AE là phân giác của \(\widehat{MAN}\)
nên AMEN là hình vuông
b: AMEN là hình vuông
=>\(\widehat{AMN}=45^0\)
=>\(\widehat{AMN}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nênMN//BC
c: Gọi O là giao điểm của AE và MN
AMEN là hình vuông
=>AE cắt MN tại trung điểm của mỗi đường và AE=MN
=>O là trung điểm chung của AE và MN và AE=MN
=>\(OA=OE=OM=ON=\dfrac{MN}{2}=\dfrac{AE}{2}\)
ΔMFN vuông tại F
mà FO là đường trung tuyến
nên \(FO=\dfrac{MN}{2}=\dfrac{AE}{2}\)
Xét ΔAFE có
FO là đường trung tuyến
\(FO=\dfrac{AE}{2}\)
Do đó: ΔAFE vuông tại F
=>\(\widehat{AFE}=90^0\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A (AB AC). Kẻ AH vuông góc với BC tại H. Qua B kẻđường thẳng vuông góc với AB, cắt đường thẳng AH tại D. Gọi tia AB và tia CD cắtnhau tại E.a) Chứng minh: BE/BA DE/DCb) Qua E kẻ đường thắng song song với AC, đường thắng này lần lượt cắt các đườngthắng AD, BC tại I, K. Chứng minh: EI EK;c) Gọi N là giao điểm của EH và AC; Gọi Q là giao điểm của DN và BC; Gọi P là giaođiểm của BN và AD. Chứng minh: NA NC và PQ // BD;d) Gọi G là giao điểm của đường thăng AQ và CD. Qua...
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Kẻ AH vuông góc với BC tại H. Qua B kẻ
đường thẳng vuông góc với AB, cắt đường thẳng AH tại D. Gọi tia AB và tia CD cắt
nhau tại E.
a) Chứng minh: BE/BA = DE/DC
b) Qua E kẻ đường thắng song song với AC, đường thắng này lần lượt cắt các đường
thắng AD, BC tại I, K. Chứng minh: EI = EK;
c) Gọi N là giao điểm của EH và AC; Gọi Q là giao điểm của DN và BC; Gọi P là giao
điểm của BN và AD. Chứng minh: NA = NC và PQ // BD;
d) Gọi G là giao điểm của đường thăng AQ và CD. Qua Q kẻ đường thăng song song
với CE, cắt đường thắng AC tại T. Chứng minh PT vuông góc AD.
mn giúp với ạ, gấp lắm, chỉ cần câu b,c thôi ạ
Cho tam giác ABC . Gọi I là giao điểm của các đường phân giác trong của các góc của tam giác . từ I kẻ IM vuông góc AB , IN vuông góc với BC , IK vuông góc với AC . Qua A kẻ đường thẳng d1 song song MN , d1 cắt đường thẳng NK tại E . Qua a kẻ đường thẳng d2 cắt MN tại D . Đường thẳng ED cắt AC , AB lần lượt tại B và Q . CHỨNG MINH P, Q là đường trung bình của tam giác ABC
1 like