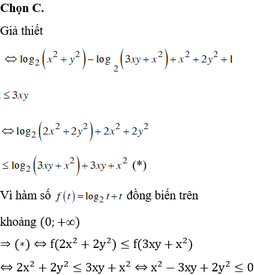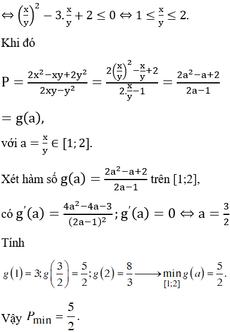Không nhìn thấy bất cứ chữ nào của đề bài cả 

\(x^2+y^2+2\left(x+y\right)-xy=0\)

\(\Leftrightarrow4x^2-4xy+4y^2+8\left(x+y\right)=0\)

\(\Leftrightarrow\left(2x-y\right)^2+4\left(2x-y\right)+4+3y^2+12y+12=-16\)

\(\Leftrightarrow\left(2x-y+2\right)^2+3\left(y+2\right)^2=-16\)

Dễ thấy VT \(\ge0\) ; VP < 0 nên phương trình vô nghiệm 

\(x^2+y^2-2\left(x+y\right)=xy\)

\(\Rightarrow x^2-2x+1+y^2-2y+1=2+xy\)

\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2=2+xy\)

Ta lại có : \(\left(x-1\right)^2+\left(y-1\right)^2\ge2\left(x-1\right)\left(y-1\right)\) (Bất đẳng thức Cauchy)

Tiếp tục phần tiếp theo

Dấu bằng xảy ra khi \(\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2=2+xy\) (vô lý vì 2=2+2.2)

⇒ Không có cặp (x;y) nguyên dương nào thỏa mãn đề bài

Ta có (1)  ⇔ x 4 + x 2 + 20 = y 2 + y

Ta thấy:  x 4 + x 2 < x 4 + x 2 + 20 ≤ x 4 + x 2 + 20 + 8 x 2 ⇔ x 2 ( x 2 + 1 ) < y ( y + 1 ) ≤ ( x 2 + 4 ) ( x 2 + 5 )

Vì x, y ∈ Z nên ta xét các trường hợp sau

+ TH1.  y ( y + 1 ) = ( x 2 + 1 ) ( x 2 + 2 ) ⇔ x 4 + x 2 + 20 = x 4 + 3 x 2 + 2 ⇔ 2 x 2 = 18 ⇔ x 2 = 9 ⇔ x = ± 3

Với  x 2 = 9   ⇒ y 2 + y = 9 2 + 9 + 20 ⇔ y 2 + y − 110 = 0 ⇔ y = 10 ; y = − 11 ( t . m )

+ TH2  y ( y + 1 ) = ( x 2 + 2 ) ( x 2 + 3 ) ⇔ x 4 + x 2 + 20 = x 4 + 5 x 2 + 6 ⇔ 4 x 2 = 14 ⇔ x 2 = 7 2   ( l o ạ i )

+ TH3: y ( y + 1 ) = ( x 2 + 3 ) ( x 2 + 4 ) ⇔ 6 x 2 = 8 ⇔ x 2 = 4 3   ( l o ạ i )

+ TH4:  y ( y + 1 ) = ( x 2 + 4 ) ( x 2 + 5 ) ⇔ 8 x 2 = 0 ⇔ x 2 = 0 ⇔ x = 0

Với  x 2 = 0  ta có  y 2 + y = 20 ⇔ y 2 + y − 20 = 0 ⇔ y = − 5 ; y = 4

Vậy PT đã cho có nghiệm nguyên (x;y) là :

(3;10), (3;-11), (-3; 10), (-3;-11), (0; -5), (0;4).

\(x^2+y^2+xy=3\)

Có \(x^2+y^2\ge2xy\) \(\Rightarrow3=x^2+y^2+xy\ge2xy+xy\) \(\Leftrightarrow xy\le1\)

\(x^2+y^2\ge-2xy\) \(\Rightarrow3=x^2+y^2+xy\ge-2xy+xy\) \(\Leftrightarrow-3\le xy\) 

Đặt A= \(x^2+y^2-xy=\left(3-xy\right)-xy=3-2xy\)

mà \(-3\le xy\le1\) \(\Rightarrow9\ge3-2xy\ge1\)

=> minA=1 <=> \(\left\{{}\begin{matrix}xy=1\\x=y\end{matrix}\right.\) <=>x=y=1

maxA=9 <=>\(\left\{{}\begin{matrix}xy=-3\\x=-y\end{matrix}\right.\) <=>\(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)

Đặt \(P=x^2+y^2-xy\)

\(\Rightarrow\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}\)

\(\dfrac{P}{3}=\dfrac{3x^2+3y^2-3xy}{3\left(x^2+y^2+xy\right)}=\dfrac{x^2+y^2+xy+2\left(x^2+y^2-2xy\right)}{3\left(x^2+y^2+xy\right)}\)

\(\dfrac{P}{3}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\Rightarrow P\ge1\)

\(P_{min}=1\) khi \(x=y=1\)

\(\dfrac{P}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)

\(\Rightarrow P\le9\)

\(P_{max}=9\) khi \(\left(x;y\right)=\left(\sqrt{3};-\sqrt{3}\right);\left(-\sqrt{3};\sqrt{3}\right)\)