tam giác abc cân có BA=BC=a AC=b đường phân giác góc A cắt BC tại M đường phân giác góc C cắt AB tại N cm MN//AC
Những câu hỏi liên quan
cho tam giác cân ABC có AB=BC đường phân giác góc A cắt BC tại M đường phân giác góc C cắt BC tại N CM MN// AC
Tam giác cân ABC có BA = BC = a, AC = b.Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Chứng minh MN // AC
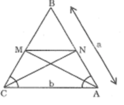
Trong △ BAC, ta có: AM là đường phân giác của (BAC)
Suy ra: 
(tỉnh chất đường phân giác) (1)
CN là đường phân giác của (BCA)
Suy ra: 
(tỉnh chất đường phân giác) (2)
Lại có: AB = CB = a (gt)
Từ (1), (2) và (gt) suy ra: 
Trong
△
BAC, ta có: 
Suy ra: MN // AC (theo định lí đảo của định lí Ta-lét).
Đúng 0
Bình luận (0)
Tam giác cân ABC có BA = BC = a, AC = b.Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N. Tính MN theo a, b.
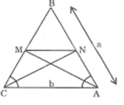
Ta có: 
(chứng minh trên)
Suy ra:
Hay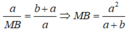 
Trong ΔBAC, ta có:
MN //AC (chứng minh trên)
Và 
Vậy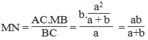 
Đúng 1
Bình luận (0)
Bài 1c) Cho tam giác ABC cân tại A, phân giác BD. Biết góc BAC120 độ. Tính các cạnh của tam giácBài 2: Cho tam giác ABC cân ở A, BC8cm, phân giác của góc B cắt đường cao AH ở K, AK/AH3/5. a) Tính độ dài AB (câu này tớ làm đc rồi)b) Đường thẳng vuông góc với BK tại B cắt AH ở E. Tính EH (còn mỗi câu này thôi)Bài 3: Cho tam giác ABC cân, có BABCa, ACb. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại Na) Cm: MN//AC b) Tính MN theo a,bBài 4: Cho tam giác ABC cân ở A, phân giác t...
Đọc tiếp
Bài 1c) Cho tam giác ABC cân tại A, phân giác BD. Biết góc BAC=120 độ. Tính các cạnh của tam giác
Bài 2: Cho tam giác ABC cân ở A, BC=8cm, phân giác của góc B cắt đường cao AH ở K, AK/AH=3/5.
a) Tính độ dài AB (câu này tớ làm đc rồi)
b) Đường thẳng vuông góc với BK tại B cắt AH ở E. Tính EH (còn mỗi câu này thôi)
Bài 3: Cho tam giác ABC cân, có BA=BC=a, AC=b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N
a) Cm: MN//AC
b) Tính MN theo a,b
Bài 4: Cho tam giác ABC cân ở A, phân giác trong BD, BC=10cm, AB=15cm
a) Tính AD, DC
b) Đường phân giác ngoài góc B của tam giác ABC cắt đường thẳng AC tại D'. Tính D'C
Bài 5: Cho tam giác ABC có AB=5cm, AC=6cm, BC=7cm. Gọi G là trọng tâm tam giác ABC, O là giao điểm của 2 đường phân giác BD, AE
a) Tính độ dài đoạn thẳng AD
b) Cm: OG//AC
HD: a) AD=2,5cm b) OG//DM => OG//AC
Bài 6: Cho tam giác ABC. Gọi I là trung điểm của cạnh BC. Đường phân giác của góc AIB cắt cạnh AB ở M. Đường phân giác của góc AIC cắt cạnh AC ở N
a) CMR: MN//BC
b) Gọi giao điểm của DE và AM là O. CM: OM=ON
c) Tam giác ABC phải thoả mãn điều kiện gì để có MN=AI
d) Tam giác ABC phải thoả mãn điều kiện gì để có MN vuông góc với AI
cho tam giác ABC cân tại B có BA=BC=a , AC =b. đường phân giác góc A cắt BC tại M , đường phân giác góc C cắt BA tại N
a ) chứng minh MN//AC
b) tính độ dài đoạn MN theo a và b
cho tâm giác cân ABC có AB=BC đường phân giắc góc A cắt BC tại M đường phân giác góc C cắt BA tại N chứng minh MN//AC
cho tâm giác cân ABC có AB=BC đường phân giắc góc A cắt BC tại M đường phân giác góc C cắt BA tại N chứng minh MN//AC
Cho tam giác ABC vuông tại A, có AB=6cm, AC=8cm và đường cao AH a. Cm tam giác ABC ~ tam giác AHB b. Tính BC,HB c. Qua B vẽ đường thẳng d vuông góc với AC, tia phân giác của góc BAC cắt BC tại M và cắt đường thẳng d tại N. Cm AB/AC= MN/AM
a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm
Đúng 0
Bình luận (0)
Cho tam giác ABC cân, có BA=BC=a, AC=b. Đường phân giác góc A cắt BC tại M, đường phân giác góc C cắt BA tại N
a) Cm: MN//AC
b) mn=???
X
a, xét tam giác ABC có CN là pg của ^ACB (gt)
=> BN/NA = BC/AC (Đl) (1)
xét tam giác ABC có AM là pg của ^BAC (gt)
=> BM/CM = AB/AC (đl) (2)
có BC = AB (gt) (3)
(1)(2)(3) => BN/NA = BM/CM
=> MN // AC (đl)