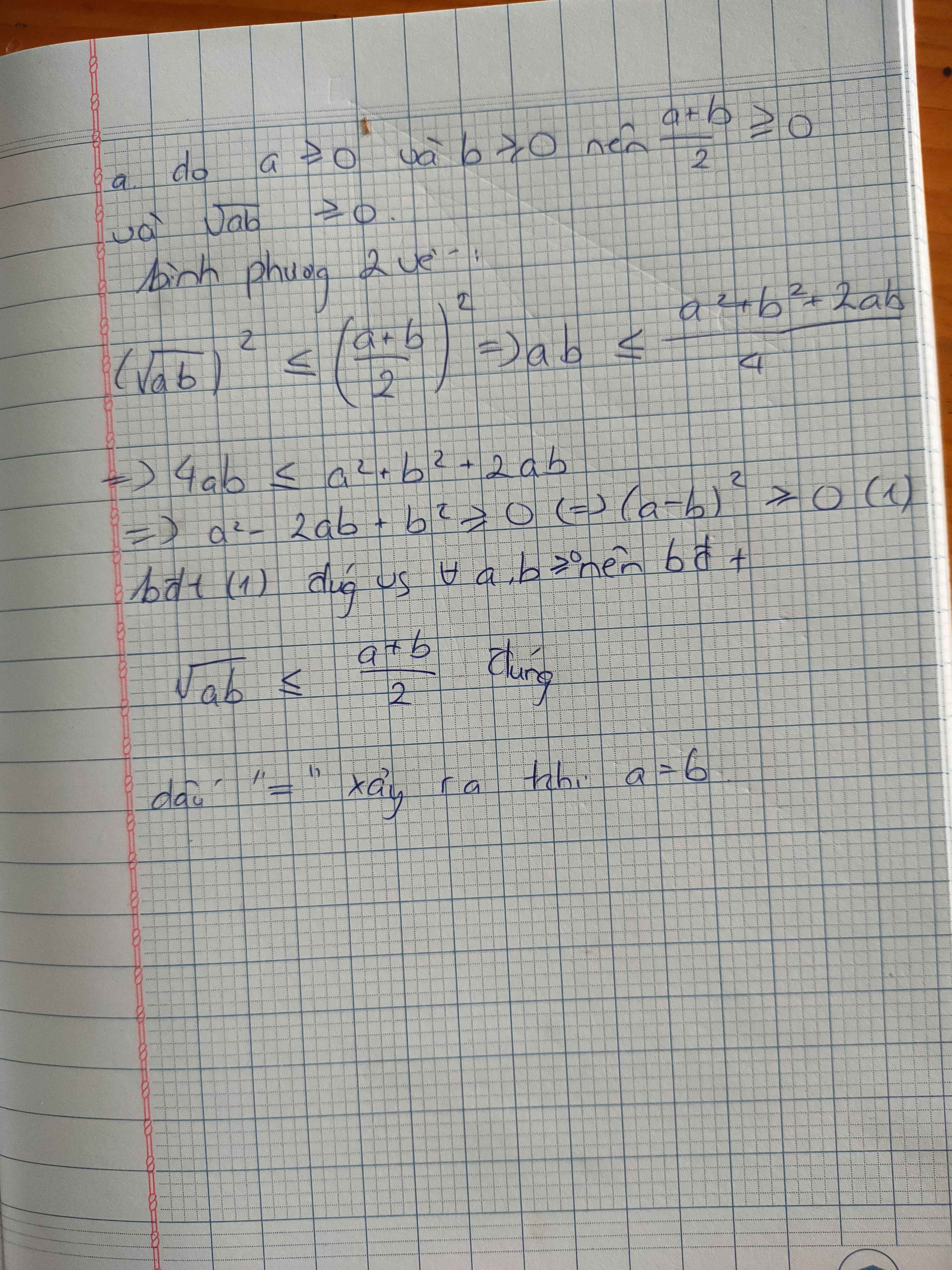Những câu hỏi liên quan
Cho tổng a+b=c. Có thể nói gì về b nếu:
a) a<0 và c>0;
b) a<0 và c=0?
cho tổng a+b=c . Có thể nói gì về số b :
a, a<0 và C >0
b, a<0 và c=0
Cho a,b,c và x,y,z khác 0 và a+b+c=0 ; x+y+z=0 ,x/a + y/b + z/c =0. CMR : a^2 . x + b^2 . y + c^2 . z
Cho a khác 0, b khác 0, c khác 0 và a+b+c=0. Tính M= \(\frac{a+b}{c}+\frac{b+c}{a}+\frac{a+c}{b}\)
a+b+c=0
=>a+b=-c;b+c=-a;a+c=-b
Thay a+b=-c;b+c=-a;a+c=-b là M ta được:\(M=\frac{-c}{c}+\frac{-a}{a}+\frac{-b}{b}=-1-1-1=-3\)
Đúng 0
Bình luận (0)
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
Đúng 2
Bình luận (0)
Cho a+c-2b=0 và 2bd-c (b+d)=0 (b, d khác 0). Chứng minh a/b=c/d
Trong không gian Oxyz, cho ba điểm A(a;0;0),B(0,b,0) và C(0;0;c),(abc≠0) Viết phương trình mặt phẳng qua ba điểm A,B và C A.
A
B
C
:
x
a
-
y
b
+
z
c
1
B. ...
Đọc tiếp
Trong không gian Oxyz, cho ba điểm A(a;0;0),B(0,b,0) và C(0;0;c),(abc≠0) Viết phương trình mặt phẳng qua ba điểm A,B và C
A. A B C : x a - y b + z c = 1
B. A B C : x a + y b + z c = 1
C. A B C : x a + y b + z c = 0
D. A B C : x a + y b + z c + 1 = 0
cho a>0,b>0,c>0 và a>b
chứng minh rằng a/b=a+c/b+c
cho 3 số a, b, c biết b<c, abc<0 và a+c=0. Hãy so sánh (a-b)(b-c)(c-a) với số 0
cho(a+b+c):(a+b-c)=(a-b+c):(a-b-c) và b khác 0.CM c=0
Từ \(\left(a+b+c\right):\left(a+b-c\right)=\left(a-b+c\right):\left(a-b-c\right)\)
\(\Rightarrow\frac{a+b+c}{a+b-c}=\frac{a-b+c}{a-b-c}=\frac{\left(a+b+c\right)-\left(a-b+c\right)}{\left(a+b-c\right)-\left(a-b-c\right)}\)
\(=\frac{a+b+c-a+b-c}{a+b-c-a+b+c}=\frac{2b}{2b}=1\)
\(\Rightarrow a+b+c=a+b-c\)\(\Rightarrow\left(a+b+c\right)-\left(a+b-c\right)=0\)
\(\Rightarrow a+b+c-a-b+c=0\)\(\Rightarrow2c=0\)\(\Rightarrow c=0\)( đpcm )