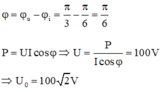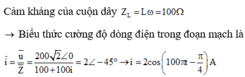Đặt điện áp xoay chiều $u=U\sqrt{2}\cos(\omega t+\phi)$ ( $U$ không đổi, $\omega$ thay đổi được). vào hai đầu đoạn mạch $AB$ mắc nối tiếp theo thứ tự gồm đoạn $AM$ chứa cuộn cảm thuần có độ tự cảm $L$, đoạn $MN$ chứa điện trở thuần $R$ và đoạn $NB$ chứa tụ điện có điện dung $C$. Khi $\omega =\omega_1$ và $\omega=\sqrt{3}\omega_1$ thì biểu thức của dòng điện trong mạch lần lượt là $i_1=I_0\cos(\omega_1t+\frac{\pi}{3})$ và $i_2=\sqrt{\frac{3}{2}}I_0\cos(\sqrt{3}\omega_1t-\frac{\pi}{12})$. Hãy tính $\frac{R^2L}{C}$
Đặt điện áp xoay chiều $uUsqrt{2}cos(omega t+phi)$ ( $U$ không đổi, $omega$ thay đổi được). vào hai đầu đoạn mạch $AB$ mắc nối tiếp theo thứ tự gồm đoạn $AM$ chứa cuộn cảm thuần có độ tự cảm $L$, đoạn $MN$ chứa điện trở thuần $R$ và đoạn $NB$ chứa tụ điện có điện dung $C$. Khi $omega omega_1$ và $omegasqrt{3}omega_1$ thì biểu thức của dòng điện trong mạch lần lượt là $i_1I_0cos(omega_1t+frac{pi}{3})$ và $i_2sqrt{frac{3}{2}}I_0cos(sqrt{3}omega_1t-frac{pi}{12})$. Hãy tính $frac{R^2L}{C}$
Đọc tiếp
*) Từ hai biểu thức dòng điện, rút ra 2 kết luận sau: khi \(\omega\) thay đổi thì
+) I cực đại tăng \(\frac{I_2}{I_1}=\sqrt{\frac{3}{2}}\Rightarrow \frac{Z_1}{Z_2}=\sqrt{\frac{3}{2}}\)
+) Pha ban đầu của i giảm 1 góc bằng: \(\frac{\pi}{3}-\left(-\frac{\pi}{12}\right)=\frac{5\pi}{12}=75^0\)
tức là hai véc tơ biểu diễn Z1 và Z2 lệch nhau 75 độ, trong đó Z2 ở vị trí cao hơn
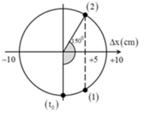
*) Dựng giản đồ véc-tơ:
Trong đó: \(\widehat{AOB}=75^0\);
Đặt ngay: \(Z_1=OB=\sqrt{\frac{3}{2}}\Rightarrow Z_2=1\)
Xét tam giác OAB có \(\widehat{AOB}=75^0;OA=1;OB=\sqrt{\frac{3}{2}}\) và đường cao OH.
Với trình độ của bạn thì thừa sức tính ngay được: \(OH=\frac{\sqrt{3}}{2}\)
\(\Rightarrow R=OH=\frac{\sqrt{3}}{2}\)
*) Tính \(Z_L,Z_C\):
\(Z_1^2=R^2+\left(Z_L-Z_C\right)^2;\left(Z_L< Z_C\right)\)
\(Z_2^2=R^2+\left(\sqrt{3}Z_L-\frac{Z_C}{\sqrt{3}}\right)^2\)
Thay số vào rồi giải hệ 2 ẩn bậc nhất, tìm được: \(Z_L=\frac{\sqrt{3}}{2};Z_C=\sqrt{3}\)
*) Tính
\(\frac{R^2L}{C}=\frac{R^2\cdot\left(L\omega_1\right)}{C\omega_1}=R^2Z_LZ_C\\ =\left(\frac{\sqrt{3}}{2}\right)^2\cdot\frac{\sqrt{3}}{2}\cdot\sqrt{3}=\frac{9}{4}\)
Đúng 2
Bình luận (2)
Đặt điện áp uU
2
cos
ωt
+
π
3
(V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức i
6
cos
ωt
+
π
6
(A) và công suất tiêu thụ của đoạn mạch bằng 150 W. Giá trị củ...
Đọc tiếp
Đặt điện áp u=U 2 cos ωt + π 3 (V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức i= 6 cos ωt + π 6 (A) và công suất tiêu thụ của đoạn mạch bằng 150 W. Giá trị của U bằng
A. 100 2 V.
B. 100 3 V.
C. 120 V.
D. 100 V.
Đáp án D
Công suất tiêu thụ của mạch điện:
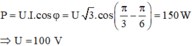
Đúng 0
Bình luận (0)
Đặt điện áp
u
U
0
cos
(
100
π
t
+
π
/
3
)
(V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức
i
√
6
cos
(...
Đọc tiếp
Đặt điện áp u = U 0 cos ( 100 π t + π / 3 ) (V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức i = √ 6 cos ( ω t + π / 6 ) ( A ) và công suất tiêu thụ của mạch là 150 W. Giá trị U0 là:
A. 100 V
B. 100 √ 3 V
C. 120 V
D. 100 √ 2 V
- Góc lệch pha giữa u và i trong mạch: φ = π/3 - π/6 = π/6.
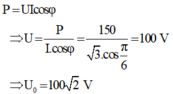
Đúng 0
Bình luận (0)
Đặt điện áp u
U
0
cos(ωt +
π
3
) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức i
6
cos(ωt +
π
6
)(A) và công suất tiêu thụ của đoạn mạch bằng 150 W. Giá trị
U
0
bằng A. 120 V. B. 100
3...
Đọc tiếp
Đặt điện áp u = U 0 cos(ωt + π 3 ) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức i = 6 cos(ωt + π 6 )(A) và công suất tiêu thụ của đoạn mạch bằng 150 W. Giá trị U 0 bằng
A. 120 V.
B. 100 3 V.
C. 100 V.
D. 100 2 V.
Có ba dụng cụ gồm điện trở thuần, R 30Ω cuộn cảm thuần L và tụ điện C. Đặt điện áp xoay chiều u U_0 c{rm{os}}({rm{w}}t + phi ) lần lượt vào hai đầu đoạn mạch nối tiếp gồm RL và RC khi đó cường độ dòng điện trong mạch i_1 6cos (wt + frac{pi }{7}) và i_2 6cos (wt + frac{{10pi }}{{21}}) Đặt điện áp trên vào hai đầu đoạn mạch RLC mắc nối tiếp thì công suất mạch điện lúc đó bằng
Đọc tiếp
Có ba dụng cụ gồm điện trở thuần, R = 30Ω cuộn cảm thuần L và tụ điện C. Đặt điện áp xoay chiều \( u = U_0 c{\rm{os}}({\rm{w}}t + \phi ) \) lần lượt vào hai đầu đoạn mạch nối tiếp gồm RL và RC khi đó cường độ dòng điện trong mạch \( i_1 = 6\cos (wt + \frac{\pi }{7}) \) và \( i_2 = 6\cos (wt + \frac{{10\pi }}{{21}}) \)Đặt điện áp trên vào hai đầu đoạn mạch RLC mắc nối tiếp thì công suất mạch điện lúc đó bằng
Khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm
1
4
π
H thì dòng điện trong đoạn mạch là dòng điện một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp
u
150
2
c
o
s
(
120
π
t
)
V thì biểu thức củ...
Đọc tiếp
Khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm 1 4 π H thì dòng điện trong đoạn mạch là dòng điện một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp u = 150 2 c o s ( 120 π t ) V thì biểu thức của cường độ dòng điện trong đoạn mạch là
![]()
![]()
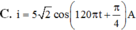
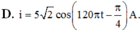
Đặt điện áp u U0cos(100πt + π/3) (V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức i √6cos(ꞷt+π/6)A và công suất tiêu thụ của mạch là 150 W. Giá trị U0 là A. 100 V B. 100√3 V C. 120 V D. 100√2 V
Đọc tiếp
Đặt điện áp u = U0cos(100πt + π/3) (V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cường độ dòng điện trong mạch có biểu thức i= √6cos(ꞷt+π/6)A và công suất tiêu thụ của mạch là 150 W. Giá trị U0 là
A. 100 V
B. 100√3 V
C. 120 V
D. 100√2 V
Đặt điện áp
u
220
2
cos
100
πt
V vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R 100
Ω
tụ điện có
C
10
-
4
2
π
F
và cuộn cảm thuần có
L
1
π
H
. Biểu thức cường độ...
Đọc tiếp
Đặt điện áp u = 220 2 cos 100 πt V vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R = 100 Ω tụ điện có C = 10 - 4 2 π F và cuộn cảm thuần có L = 1 π H . Biểu thức cường độ dòng điện trong đoạn mạch là:
A. i = 2 , 2 cos 100 πt - π 4 A
B. i = 2 , 2 2 cos 100 πt - π 4 A
C. i = 2 , 2 cos 100 πt + π 4 A
D. i = 2 , 2 2 cos 100 πt + π 4 A
Đặt điện áp
u
200
2
cos
(
100
π
t
)
V
vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần
100
Ω
và cuộn cảm thuần có độ tự cảm
1
π
H
Biểu thức cường độ dòng điện trong đoạn mạch là A.
i
2
2
cos
(
100
πt...
Đọc tiếp
Đặt điện áp u = 200 2 cos ( 100 π t ) V vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần 100 Ω và cuộn cảm thuần có độ tự cảm 1 π H Biểu thức cường độ dòng điện trong đoạn mạch là
A. i = 2 2 cos ( 100 πt + π 4 ) (A)
B. i = 2 cos ( 100 πt - π 4 ) (A)
C. i = 2 cos ( 100 πt + π 4 ) (A)
D. i = 2 2 cos ( 100 πt - π 4 ) (A)
Đặt điện áp
u
200
2
cos
(
100
π
t
)
V
vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần 100 Ω và cuộn cảm thuần có độ tự cảm
1
π
H
. Biểu thức cường độ dòng điện trong đoạn mạch là A.
i
2
2
cos
(...
Đọc tiếp
Đặt điện áp u = 200 2 cos ( 100 π t ) V vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần 100 Ω và cuộn cảm thuần có độ tự cảm 1 π H . Biểu thức cường độ dòng điện trong đoạn mạch là
A. i = 2 2 cos ( 100 π t + π 4 ) ( A )
B. i = 2 cos 100 π t - π 4 ( A )
C. i = 2 cos 100 π t + π 4 ( A )
D. i = 2 2 cos 100 π t - π 4 ( A )
Đáp án B
Cách giải:
+ Cảm kháng của cuộn dây Z L = L ω = 100
Biểu diễn phức dòng điện trong mạch
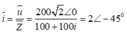
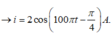
Đúng 0
Bình luận (0)