giúp mình với ạ !
Ai giúp mình với
A=10^2022-1 chứng minh A chia hết cho 11
Mọi người giúp mình với ạ
Lời giải:
Ta có:
$10\equiv -1\pmod {11}$
$\Rightarrow 10^{2022}\equiv (-1)^{2022}\equiv 1\pmod {11}$
$\Rightarrow A=10^{2022}-1\equiv 1-1\equiv 0\pmod {11}$
Vậy $A\vdots 11$
ok
A= 10^2022-1
Ta có thể thấy 10^2022=100000000...........0000000000
10000000.......0000000000-1 thì lúc nnày tổng bằng
9999999999999999........................999999999999999999999
mà 99999999999999999999999....................9999999999999999999chia hết cho 11 nên tổng này chia hết cho 11
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
A = 1+ 1 phần 2+ 1 phần 3+...+1 phần 255<8
giúp mình với mình cần gấp
giúp câu trả lời cho nguyễn thu ánh!!![]()
mọi người giúp mình với, mẹ mình đang mắng mình giúp mình
giúp mình với
.... you [be] .......... a food student
các bạn ơi giúp mình câu này với mình học lớp 5
Wish you be a good student
Không biết đúng không. Đúng thì k nha
Giúp mình với !!!
2 nút lệnh A-Z , Z-A nằm ở đâu ?
Bạn nào biết thì giúp mình với nhé!!!
Cảm ơn các bạn, yêu các bạn![]()
![]()
![]()
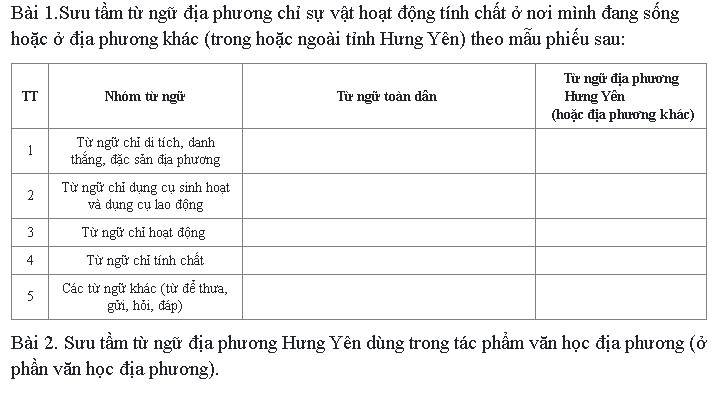
Giúp mình với a mình cần gấp
 A-Ai cứu mình với...bài nhiều quá...mình không làm nổi...Mấy bạn giúp mình với...
A-Ai cứu mình với...bài nhiều quá...mình không làm nổi...Mấy bạn giúp mình với...
giúp mình với ạ (nếu được giải chi tiết câu a cho mình với mình cảm ơn)
a: \(A=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x+\sqrt{x}+1}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)+1=x-\sqrt{x}+1\)
b:
\(\dfrac{x}{12}=\dfrac{\left(\sqrt{5}+2\right)\sqrt[3]{17\sqrt{5}-38}}{\sqrt{5}+\sqrt{14-6\sqrt{5}}}\)
\(\Leftrightarrow x\cdot\dfrac{1}{12}=\dfrac{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}{\sqrt{5}+3-\sqrt{5}}\)
\(\Leftrightarrow\dfrac{x}{12}=\dfrac{1}{3}\)
=>x=36
Khi x=36 thì \(A=36-6+1=37-6=31\)
c: \(B=\dfrac{2\sqrt{x}}{A}=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}\)
\(B-2=\dfrac{2\sqrt{x}-2x+2\sqrt{x}-2}{x-\sqrt{x}+1}\)
\(=\dfrac{-2x+4\sqrt{x}-2}{x-\sqrt{x}+1}=\dfrac{-2\left(x-2\sqrt{x}+1\right)}{x-\sqrt{x}+1}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}}< 0\)
=>B<2
\(2\sqrt{x}>0;x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
=>B>0
=>0<B<2
tính giá trị nhỏ nhất A=|x-3|+11
Can ai giúp mình với toán 6 nha,giúp mình với ^-^
Đề
GTLN hay GTNN
gia trị nhỏ nhất nha
Ta có : \(\left|x-3\right|\ge0\) với mọi x
\(\Rightarrow\left|x-3\right|+11\ge11\) với mọi x
\(\Rightarrow A\ge11\) với mọi x
\(\Rightarrow GTNN\) của \(A=11\)
Dấu " = " xảy ra
\(\Leftrightarrow\left|x-3\right|=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(GTNN\) của \(A=11\) \(\Leftrightarrow x=3\)