Bài 1: Cho tam giác ABC có \(\widehat{A}=80^o,\widehat{B}=50^o\)
a) Chứng minh tam giác ABC cân
b) Đường thẳng song song với BC cắt tia đối của tia AB ở D, cắt tia đối của tia AC ở E. Chứng minh tam giác ADE cân.
bài1 Cho tam giác ABC cân tại A .D là điểm trên cạnh ac .đường thẳng qua d song song với AB cắt BC tại E Chứng minh tam giác dec cân
bai2 Cho tam giác ABC có A bằng 80 độ B bằng 50 độ
a chứng minh tam giác ABC cân
B đường thẳng song song với BC cắt tia đối của tia AB tại D cắt tia đối của tia AC tại E Chứng minh tam giác ade cân
bai3 Cho tam giác ABC cân tại A đường thẳng song song với b c cắt các cạnh AB AC lần lượt tại d và e Gọi O là giao điểm của Be và CD Chứng minh
a tam giác ade cân
B tam giác OBC cân
cac bqn lam nhanh giup minh minh dang can gqp
b1 :
DE // AB
=> góc ABC = góc DEC (đồng vị)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc DEC = góc ACB
=> tam giác DEC cân tại D (dh)
b2:
a, tam giác ABC => góc A + góc B + góc C = 180 (đl)
góc A = 80; góc B = 50
=> góc C = 50
=> góc B = góc C
=> tam giác ABC cân tại A (dh)
b, DE // BC
=> góc EDA = góc ABC (slt)
góc DEA = góc ECB (dlt)
góc ABC = góc ACB (Câu a)
=> góc EDA = góc DEA
=> tam giác DEA cân tại A (dh)
1. Cho tam giác MNP có góc M = 40 độ, góc N = 100 độ. Chứng minh tam giác MNP là tam giác cân.
2. Cho tam giác ABC có góc A = 80 độ, góc B = 50 độ. Đường thẳng song song với BC cắt tia đối của tia AB tại D và cắt tia đối của tia AC tại E. Chứng minh rằng tam giác ADE là tam giác cân
Bài 1:
Tam giác MNP có: \(\widehat{M}=40^o;\widehat{N}=100^o\)
Tổng số đo 3 góc của 1 tam giác là 180o, ta được:
\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\\ \Leftrightarrow40^o+100^o+\widehat{P}=180^o\\ \Leftrightarrow140^o+\widehat{P}=180^o\\ \Leftrightarrow\widehat{P}=180^o-140^o=40^o\)
Vì: \(\widehat{M}=\widehat{P}=40^o\) => Tam giác MNP là tam giác cân tại N (ĐPCM)
Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D. Từ D kẻ đường thẳng song song với BC cắt tia đối AC tại E. Hai tia phan giác của hai góc AED và góc ABC cắt nhau tại O.
Chứng minh góc BOE = \(\frac{1}{2}\) ( \(\widehat{ABC}+\widehat{ACB}\)
Kẻ OF//BC(F thuộc AC)
=>OF//DE//BC
DE//BC
=>góc DEA=góc ACB
=>góc DEO=1/2*góc ACB
ED//OF
=>góc DEA=góc CFD và góc DEO=góc EOF
=>góc EOF=1/2*góc ACB
=>góc DEO=góc EOF
OF//BC
=>góc FOB=góc OBC=1/2góc ABC
góc BOE=góc BOF+góc EOF
=1/2(góc ABC+góc ACB)
Cho tam giác ABC có \(\widehat{A}=120^o\) goi AD là tia phân giác của \(\widehat{BAC}\) (D thuộc BC) . Trên tia đối của tia AB lấy điểm E, trên tia đối của tia AC lấy điểm F sao cho AE=AF=AD.
a,Chứng minh tam giác DEF là tam giác đều
b, Qua A vẽ đường thẳng song song với BC cắt BF ,CE lần lượt tại M,N. Chứng minh : AM+CN=AN+BM
Cho tam giác ABC có \(\widehat{A}=60^o\), kẻ tia phân giác của góc B cắt AC tại D, tia phân giác của góc C cắt AB ở E. Qua A kẻ đường thẳng song song với CE, đường thẳng này cắt đường thẳng BC tại F.
a, Chứng minh rằng : \(\widehat{AFC}=\widehat{CAF}\)
b, Chứng minh rằng : \(\widehat{BDC}=\widehat{AEC}\)
Cho tam giác ABC có góc A = 80 độ. góc B= 50 độ.Chứng minh rằng:
a.Tam giác ABC cân
b.Đường thẳng song song với BC cắt tia đối của hai tia AB ở D,cắt tia đối của tia AC ở E.Chứng minh rằng:Tam giác ADE cân
a, Vì góc A + góc B + góc C = 180 độ
=> góc C = 180 độ - góc A - góc B = 180 độ - 80 độ - 50 độ = 50 độ
=> góc B = góc C
=> t/g ABC cân
b, Ta có: góc ADE = góc ABC
góc AED = góc ACB
Mà góc ABC = góc ACB (vì t/g ABC cân)
=> góc ADE = góc AED
=> t/g ADE cân
sửa
b, Ta có: góc ADE = góc ABC (đồng vị)
góc AED = góc ACB (đồng vị)
Mà góc ABC = góc ACB (vì t/g ABC cân)
=> góc ADE = góc AED
=> t/g ADE cân
a) Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
80o+50o+\(\widehat{B}\)=180o
\(\widehat{B}\)=180o-(80o+50o)
\(\widehat{B}\)=180o-140o
\(\widehat{B}\)=50o
Vì \(\widehat{B}\)=\(\widehat{C}\) => \(\Delta\)ABC cân tại A
b)Vì DE//BC nên ta có :
\(\widehat{ADE}=\widehat{ABC}\) ( 2 góc đồng vị )
\(\widehat{AED}=\widehat{ACB}\) ( 2 góc đồng vị )
=> \(\widehat{ADE}=\widehat{AED}\)
=> \(\Delta\)ADE cân tại A
Cho tam giác ABC cân tại A, các đường thẳng qua B vuông góc với AB và qua C vuông góc với AC cắt nhau tại S
a) Chứng minh tam giác SBC cân
b) Trên tia đối của tia BS lấy điểm D, trên tia đối của tia CS lấy điểm E sao cho CE=BD. Chứng minh rằng DE song song BC
Bài 3: Cho tam giác ABC. Vẽ ra phía ngoài tam giác ABC các tam giác vuông cân ở A là ABD và ACE. Dựng AH vuông góc với BC, đường thẳng HA cắt DE ở K. Dựng AI vuông góc với DE, đường thẳng IA cắt BC tại M. Chứng minh rằng:
a) Tam giác AEK = Tam giác CAM
b) KD = KE
Cho tam giác ABC. Trên tia đối của BC lấy điểm D, trên tia đối của CB lấy điểm E sao cho BD=BC=CE. Qua D kẻ đường thẳng song song ới AB cắt AC ở H. Qua E kẻ đường thẳng song song với AC cắt AB ở K,chúng cắt nhau ở I.
a) Tứ giác BHKC là hình gì? Vì sao ?
b) Tia IA cắt BC ở M. Chứng minh MB=MC
c) Tìm điều kiện của tam giác ABC để tứ giác DHKE là hình thang cân
a: Xét ΔBNQ có
C là trung điểm của BQ
CA//NQ
Do đó: A là trung điểm của NB
Xét ΔCPM có
B là trung điểm của CP
CA//MP
DO đó: A là trung điểm của CM
Xét tứ giác BMNC có
A là trung điểm chung của BN và MC
nên BMNC là hình bình hành
b: Để ANKM là hình bình hành
nên AM//KN và AN//KM
=>AB//MK và AB=MK
=>ABMK là hình bình hành
=>AI//BM
Xét ΔCBM có
A là trung điểm của CA
AI//BM
DO đó; I là trung điểm của BC
Cho tam giác ABC có \(\widehat A = 120^\circ \). Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.
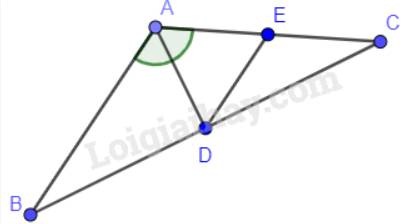
\(\widehat A = 120^\circ \)nên \(\widehat {DAE} = 60^\circ \)(AD là phân giác của góc A).
Ta có: DE // AB nên \(\widehat {CED} = \widehat {EAB} = 120^\circ \)(hai góc đồng vị). Ba điểm A, E, C thẳng hàng nên góc AEC bằng 180°
\(\Rightarrow \widehat {AED} = 180^\circ - \widehat {CED} = 180^\circ - 120^\circ = 60^\circ \)
Tam giác ADE có \(\widehat {EAD} = \widehat {ADE}\) (\(=60^0\)) nên là tam giác cân.
Mà \(\widehat {DEA} = 60^\circ \)
Do đó, tam giác ADE đều ( tam giác cân có 1 góc bằng \(60^0\)).