cho tam giác vuông tại A tia BD là tia phân giác của góc B kẻ DE vuông góc với BC. Chứng minh BA=BE

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A.Vẽ tia BD là tia phân giác của góc B. Trên BC lấy điểm E sao cho BE=AB. a)Chứng minh tam giác ABD = tam giác EBD,DE vuông góc với BC,Kẻ AH vuông góc với BC. Chứng minh góc BAH = góc ACH và AH song song với DE
cho tam giác ABC vuông tại A; BD là phân giác của góc B (D thuộc AC). trên tia BC lấy điểm E sao cho BA = BE. a) chứng minh rằng: tam giác ABD = tam giác EBD và DE vuông góc với BE. b) chứng minh: BD là đường trung trực của đoạn tthẳng AE. c) Kẻ AH vuông góc với BC tại H. CHỨNG minh rằng: AD < DH

a)
và có:
BA = BE (gt)
(BD là tia phân giác góc B)
BD là cạnh chung
(c.g.c)
(hai góc tương ứng)
DE BE
b) và có:
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ đường phân giác BD, kẻ DE vuông góc với BC (E thuộc BC). a) Chứng minh rằng: BD là trung trực của AE và AD DC. b) Tia ED cắt tia BA tại F. Chứng minh: BD vuông góc với CF và AE // CF.c) Tia BD cắt FC tại G. Chứng minh rằng D cách đều ba cạnh của tam giác AEG. d) Lấy M và N tương ứng di động trên BF và BC sao cho BM + BN BC. Chứng minh rằng trung điểm I của MN luôn nằm trên một đường thẳng cố định.Chỉ cần làm phần c,d
Đọc tiếp
Cho tam giác ABC vuông tại A. Kẻ đường phân giác BD, kẻ DE vuông góc với BC (E thuộc BC). a) Chứng minh rằng: BD là trung trực của AE và AD < DC. b) Tia ED cắt tia BA tại F. Chứng minh: BD vuông góc với CF và AE // CF.c) Tia BD cắt FC tại G. Chứng minh rằng D cách đều ba cạnh của tam giác AEG. d) Lấy M và N tương ứng di động trên BF và BC sao cho BM + BN = BC. Chứng minh rằng trung điểm I của MN luôn nằm trên một đường thẳng cố định.
Chỉ cần làm phần c,d
c) -△ABG và △JBG có: \(AB=BE;\widehat{ABG}=\widehat{JBG};BG\) là cạnh chung.
\(\Rightarrow\)△ABG=△JBG (c-g-c).
\(\Rightarrow\widehat{AGB}=\widehat{JGB}\) nên GB là tia phân giác góc AGE.
AE//CF \(\Rightarrow\widehat{BAE}=\widehat{AFG}\).
-△BFC cân tại B mà BG là đường cao nên BG cũng là trung tuyến.
\(\Rightarrow\)G là trung điểm CF.
-△ACF vuông tại A có: AG là trung tuyến.
\(\Rightarrow AG=FG=\dfrac{1}{2}BC\Rightarrow\)△AFG cân tại G.
\(\Rightarrow\widehat{AFG}=\widehat{FAG}\) mà \(\widehat{BAE}=\widehat{AFG}\Rightarrow\widehat{BAE}=\widehat{FAG}\).
\(\widehat{EAC}=90^0-\widehat{BAE}=90^0-\widehat{FAG}=\widehat{GAC}\).
\(\Rightarrow\)AC là tia phân giác góc EAG.
-△AEG có: 2 đg phân giác AC và GB cắt nhau tại D.
\(\Rightarrow\)D là điểm cách đều 3 cạnh của △AEG (hay còn gọi là giao của 3 đg phân giác, tâm đường tròn nội tiếp tam giác).
Đúng 0
Bình luận (1)
d) -Cho mình xin sử dụng t/c của lớp 8, mình sẽ c/m sau (đường trung bình của tam giác).
\(BM+BN=BC\) mà \(BM+MF=BF=BC\Rightarrow MF=BN\).
-Gọi H là trung điểm BC. Qua M kẻ đường thẳng song song với IH cắt BC tại J.
-△NMJ có: IH//MJ, I là trung điểm MN.
\(\Rightarrow\)H là trung điểm NJ nên \(NH=HJ\).
\(CJ=CH-HJ=BH-NH=BN\)
\(\Rightarrow CJ=MF\Rightarrow BM=BJ\Rightarrow\)△MBJ cân tại B.
\(\Rightarrow\widehat{BMJ}=\dfrac{180^0-\widehat{MBJ}}{2}\) mà \(\widehat{BAE}=\dfrac{180^0-\widehat{MBJ}}{2}\)
\(\Rightarrow\widehat{BMJ}=\widehat{BAE}\Rightarrow\)MJ//AE.
-Ta dễ dàng thấy rằng điểm A,D,E cố định \(\Rightarrow\)AE, MJ cố định.
\(\Rightarrow\)Trung điểm I của MN luôn nằm trên 1 đg thẳng cố định (đg thẳng MJ).
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A. Tia BD là tia phân giác của góc B,kẻ DE vuông góc với BC.Chứng minh BA=BE
Giai :
Tự vẽ hình nha pn
Xét tam giác BAD ,BED CÓ
BD chung
góc B1= góc B (gt)
góc A=góc D =90độ
=> tam giác BAD= BED ( cạnh huyền ,góc nhọn)
=>BA=BE
Đúng 0
Bình luận (0)
lm gấp giúp mình bài này nhé Đề bài 1 : cho tam giác ABC vuông tại A . Kẻ BD là tia phân giác của góc ABC . Trên cạnh BC lấy điểm E sao cho BE = BA . a) chứng minh Tam giác ABD = tam giác EBD b) chứng minh DE = AD và DE vuông góc với BC ( hình dưới phần bình luận )
a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: ΔBAD=ΔBED
=>DA=DE và \(\widehat{BAD}=\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Đúng 1
Bình luận (0)
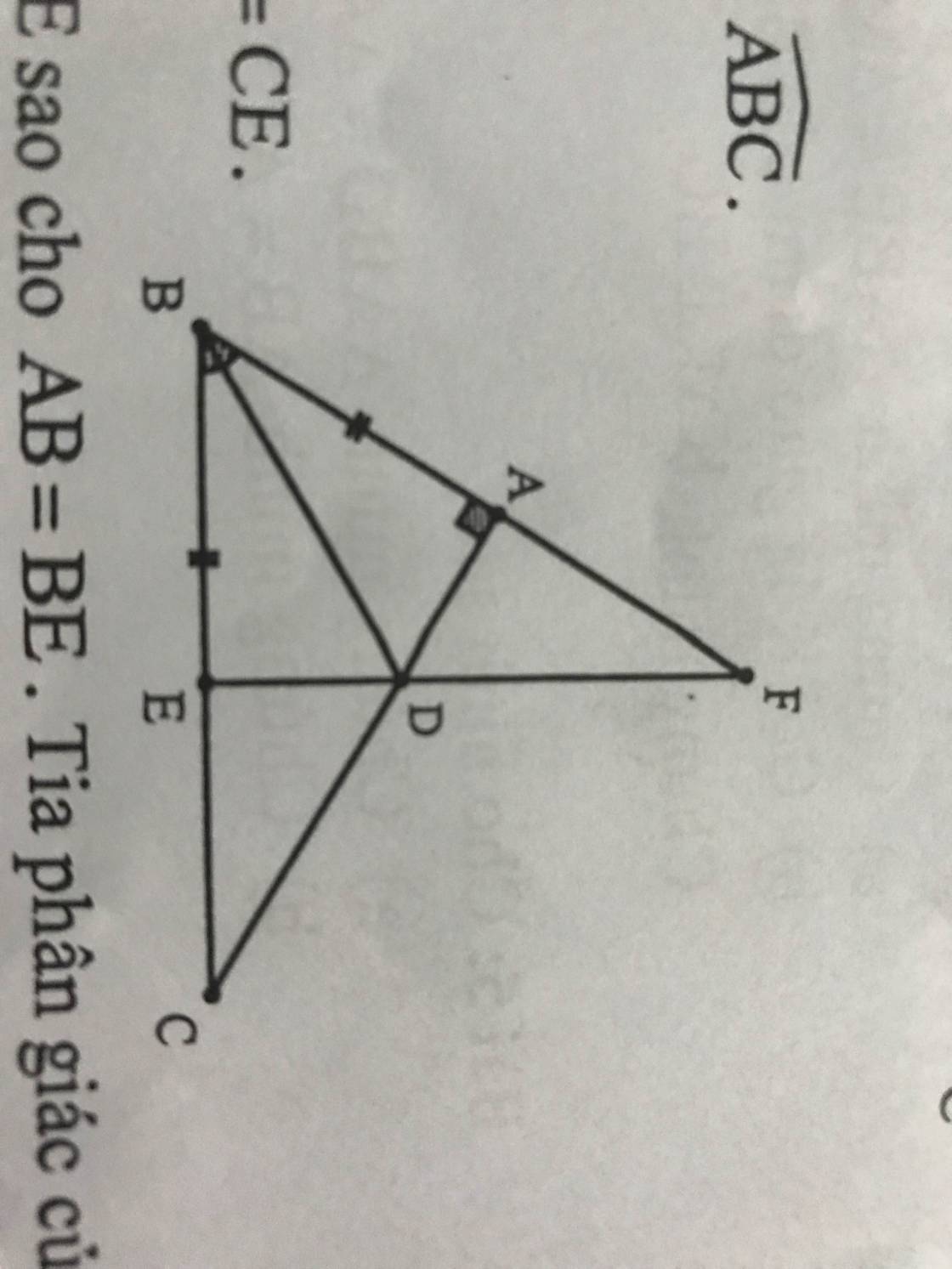
 chỉ lm phần a và b bài 12 thui nhé , hình bên cạnh nhé
chỉ lm phần a và b bài 12 thui nhé , hình bên cạnh nhé
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và AB ( AC trên cạnh BC lấy điểm E sao cho BE BA, kẻ BD là tia phân giác của góc ABC ( D thuộc AC )a, tam giác ABE là tam giác gì ? chứng minh tam giác ABD tam giác EBDb, chứng minh DE vuông góc với BCc,chứng minh BD là đường trung trực của AEGiúp mình sớm sớm ạ mai mình thi rồi . Cảm ơn rất nhiều
Đọc tiếp
Cho tam giác ABC vuông tại A và AB ( AC trên cạnh BC lấy điểm E sao cho BE = BA, kẻ BD là tia phân giác của góc ABC ( D thuộc AC )
a, tam giác ABE là tam giác gì ? chứng minh tam giác ABD = tam giác EBD
b, chứng minh DE vuông góc với BC
c,chứng minh BD là đường trung trực của AE
Giúp mình sớm sớm ạ mai mình thi rồi . Cảm ơn rất nhiều
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đó: ΔBAD=ΔBED
=>BA=BE
=>ΔBAE cân tại B
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc với BC
c: ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
Đúng 2
Bình luận (1)
a, tam giác ABE là tam giác gì ? chứng minh tam giác ABD = tam giác EBD
b, chứng minh DE vuông góc với BC
c,chứng minh BD là đường trung trực của AE
( Lưu ý : chỉ yêu cầu vẽ hình ) mọi người giúp mình với , mai mình thi rồi
Câu 1: Cho tam giác ABC có góc A 90 độ. kẻ AH vuông góc với BC (H e BC) Trên đường vuông góc với BC tại điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AHBD chứng minh a) tam giác AHBDBH b) hai đường thẳng AB và DH có song song không? vì sao?Câu 2: Cho góc nhọn xOy. Trên tia Ox lấy điểm A, lấy điểm B trên tia Oy sao cho OAOB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho ACBD chứng minh ADBC. gọi E là giao điểm AD và BC, chứng minh tam giác EADEBD.Câu 3: Cho tam giác ABC vuông...
Đọc tiếp
Câu 1: Cho tam giác ABC có góc A= 90 độ. kẻ AH vuông góc với BC (H e BC) Trên đường vuông góc với BC tại điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho AH=BD chứng minh a) tam giác AHB=DBH b) hai đường thẳng AB và DH có song song không? vì sao?
Câu 2: Cho góc nhọn xOy. Trên tia Ox lấy điểm A, lấy điểm B trên tia Oy sao cho OA=OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC=BD chứng minh AD=BC. gọi E là giao điểm AD và BC, chứng minh tam giác EAD=EBD.
Câu 3: Cho tam giác ABC vuông tại A, kẻ phân giác BD (D e AC), kẻ DE vuông góc với BC tại E. Chứng minh BA=BE
Câu 4: Cho tam giác ABC vuông tại A, kẻ phân giác BD (D e AC), kẻ DE vuông góc với BC tại E. gọi F là giao điểm của tia BA và ED. chứng minh tam giác BDA=BDE và DC=DF
Giúp mình giải lun nhé. Giúp mình đi mình Tick cho!!!
Cho tam giác ABC vuông tại A có BE là tia phân giác của góc B ( E thuộc AC). Từ E kẻ ED vuông góc với BC tại D.
a) Chứng minh ΔABE = ΔDBE.
b) Chứng minh BE⊥AD
c) Gọi F là giao điểm của tia BA và tia DE. Chứng minh tam giác EFC cân tại E.
help pls ![]()
a: Xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔABE=ΔDBE
b: Ta có: ΔABE=ΔDBE
=>BA=BD và EA=ED
Ta có: BA=BD
=>B nằm trên đường trung trực của AD(1)
Ta có: EA=ED
=>E nằm trên đường trung trực của AD(2)
Từ (1) và (2) suy ra BE là đường trung trực của AD
=>BE\(\perp\)AD
c: Xét ΔEAF vuông tại A và ΔEDC vuông tại D có
EA=ED
\(\widehat{AEF}=\widehat{DEC}\)(hai góc đối đỉnh)
Do đó: ΔEAF=ΔEDC
=>EF=EC
=>ΔEFC cân tại E
Đúng 0
Bình luận (0)


















