Gọi cạnh của tam giác là a, trung điểm BC là I.

+Ta có: \(BC=a\sqrt{2};\text{ }IB=IC=\frac{IA}{2}=\frac{a}{\sqrt{2}}\)

+Ta có: \(MB^2+MC^2=\left(\frac{a}{\sqrt{2}}-IM\right)^2+\left(\frac{a}{\sqrt{2}}+IM\right)^2=a^2+2IM^2\text{ (1)}\)

+AI vừa là trung tuyến vừa là phân giác góc A nên AI là trung trực tam giác ABC.

=> Tam giác AIM vuông tại I

\(\Rightarrow AM^2=AI^2+IM^2=\left(\frac{a}{\sqrt{2}}\right)^2+IM^2=\frac{a^2}{2}+IM^2\)

\(\Rightarrow2AM^2=a^2+2IM^2\text{ (2)}\)

Từ (1) và (2) suy ra \(MB^2+MC^2=2MA^2\)

Gọi cạnh của tam giác là a, trung điểm BC là I.

+Ta có: BC=a√2; IB=IC=IA2 =a√2 

+Ta có: MB2+MC2=(a√2 −IM)2+(a√2 +IM)2=a2+2IM2 (1)

+AI vừa là trung tuyến vừa là phân giác góc A nên AI là trung trực tam giác ABC.

=> Tam giác AIM vuông tại I

⇒AM2=AI2+IM2=(a√2 )2+IM2=a22 +IM2

⇒2AM2=a2+2IM2 (2)

Từ (1) và (2) suy ra MB2+MC2=2MA2

Lấy thêm trung điểm K của BC rồi dùng định lý Pytago tính các cạnh MB, MC, MA theo AB, AC, BC, AK

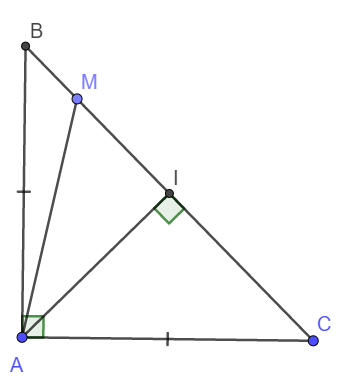
Đặt AB = AC = a \(\Rightarrow BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)

Gọi I là trung điểm BC, do tam giác ABC cân nên AI cũng là đường cao.

\(AI=BI=IC=\frac{a\sqrt{2}}{2}\)

Đặt MI = x ( 0 < x < \(\frac{a\sqrt{2}}{2}\) )

Ta có \(BM^2=\left(BI-MI\right)^2=\left(\frac{a\sqrt{2}}{2}-x\right)^2\)

\(MC^2=\left(IC+MI\right)^2=\left(\frac{a\sqrt{2}}{2}+x\right)^2\)

\(\Rightarrow MB^2+MC^2=2\left(\frac{a^2}{2}+x^2\right)=2\left(AI^2+MI^2\right)\)

\(=2AM^2\)

Vậy nên ta đã chứng minh được \(\forall M\in BC:BM^2+MC^2=2AM^2\)

Ngoài cách của cô Huyền ra, mình còn có thêm một cách như sau:

Gọi D và E lần lượt là hình chiếu của M lên AB và AC.

Xét tam giác MDB vuông tại B có \(\widehat{MBD}=45^o\)

\(\Rightarrow\)\(\Delta MDB\) vuông cân tại D

\(\Rightarrow\)\(MB^2=2MD^2\)

Tương tự ta có \(MC^2=2ME^2\)

Cộng vế theo vế ta được:

\(MB^2+MC^2=2MD^2+2ME^2\)

\(\Rightarrow\)\(MB^2+MC^2=2MA^2\left(đpcm\right)\)

Từ MM kẻ MEME vuông góc với ABAB, MFMF vuông góc với ACAC.

Ta có ΔEBMΔEBM vuông cân tại EE, ΔFMCΔFMC vuông cân tại FF và AEMFAEMF là hình chữ nhật.

Áp dụng định lý PytagoPytago vào các tam giác EBM,FMC,AEFEBM,FMC,AEF, ta có:

BM2=EM2+BE2=2ME2;MC2=2FM2⇒BM2+MC2=2(ME2+MF2)BM2=EM2+BE2=2ME2;MC2=2FM2⇒BM2+MC2=2(ME2+MF2)                (1)

Mà AM2=EF2=ME2+MF2AM2=EF2=ME2+MF2             (2)

Từ (1),(2)(1),(2) ta có dpcmdpcm

Từ MM kẻ ME vuông góc với ABAB, MFMF vuông góc với ACAC.

Ta có ΔEBM vuông cân tại E, ΔFMC vuông cân tại F và AEMF là hình chữ nhật.

Áp dụng định lý Pytago vào các tam giác EBM,FMC,AEF, ta có:

BM2=EM2+BE2=2ME2;MC2=2FM2⇒BM2+MC2=2(ME2+MF2)BM2=EM2+BE2=2ME2;MC2=2FM2⇒BM2+MC2=2(ME2+MF2)                (1)

Mà AM2=EF2=ME2+MF2AM2=EF2=ME2+MF2             (2)

Từ (1),(2)(1),(2) ta có dpcm