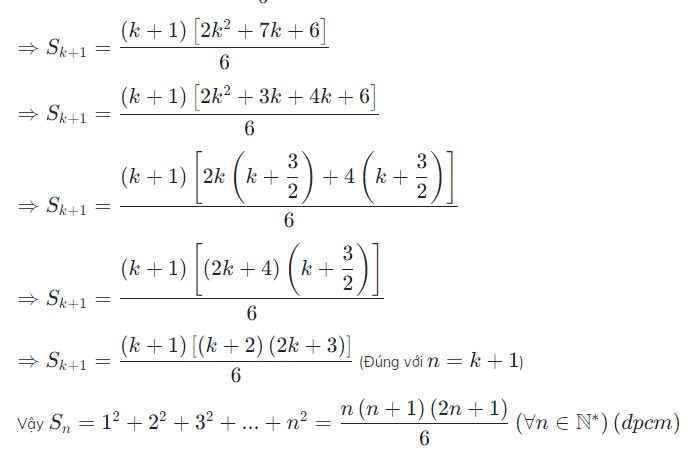Chứng minh rằng BCNN(n,2019n2 + 1)=2019n2 + n với mọi số tự nhiên n khắc 0

Những câu hỏi liên quan
Chứng minh rằng : BCNN ( n ; 37n + 1 ) = 37n^2 + n với mọi số tự nhiên n
Bài tập : Chứng minh rằng : BCNN ( n ; 37n + 1 ) = 37n^2 + n với mọi số tự nhiên lớn hơn 0
GIÚP MÌNH VỚI ! AI NHANH VÀ ĐÚNG CHO 3 TICK !
*Xét n=1
=> 37n+1 chia hết cho 1
*Xét n>1
=> 37n+1 không chia hết cho n
Vậy BCNN (n;37n+1) = n(37n+1)= 37n2 + . với mọi n > 0
Chứng tỏ rằng: BCNN(n,37n+1)=37n^2+n với mọi số tự nhiên n Giúp mình với ạ
(f) Chứng minh rằng với mọi số tự nhiên n 1 thì: 5^n+2 + 26.5^n + 82n+1 chia hết cho 59.(g) Chứng minh rằng với mọi số tự nhiên n 1 thì số 4^2n+1 + 3^n+2chia hết cho 13.(h) Chứng minh rằng với mọi số tự nhiên n 1 thì số 5^2n+1 + 2^n+4+ 2^n+1 chia hết cho 23.(i) Chứng minh rằng với mọi số tự nhiên n 1 thì số 11n+2 + 122n+1 chia hết cho 133.(j) Chứng minh rằng với mọi số tự nhiên n 1: 5^2n−1 .26n+1 + 3^n+1 .2^2n−1 chia hết cho 38
Đọc tiếp
(f) Chứng minh rằng với mọi số tự nhiên n > 1 thì: 5^n+2 + 26.5^n + 82n+1 chia hết cho 59.
(g) Chứng minh rằng với mọi số tự nhiên n > 1 thì số 4^2n+1 + 3^n+2chia hết cho 13.
(h) Chứng minh rằng với mọi số tự nhiên n > 1 thì số 5^2n+1 + 2^n+4+ 2^n+1 chia hết cho 23.
(i) Chứng minh rằng với mọi số tự nhiên n > 1 thì số 11n+2 + 122n+1 chia hết cho 133.
(j) Chứng minh rằng với mọi số tự nhiên n > 1: 5^2n−1 .26n+1 + 3^n+1 .2^2n−1 chia hết cho 38
1+2+3+4+5+6+7+8+9=133456 hi hi
đào xuân anh sao mày gi sai hả
???????????????????
Xem thêm câu trả lời
Chứng minh rằng với mọi số tự nhiên n khác 0 ta luôn có :
1² + 2² + 3² + .... + n² = n . (n+1).(2n+1)/6
a) Chững minh rằng BCNN (n;37n +1 ) = 37n^2 với mọi số tự nhiên n lớn hơn 0
b) Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng ; a chia cho 9 dư 3; a chia cho 27 dư 12
Làm nhanh giúp mik vs ạ!!!!!!!!!
Answer:
a) Ta đặt \(a=\left(n;37n+1\right)\) \(\left(a\inℕ^∗\right)\)
Ta có: n chia hết cho a
=> 37n chia hết cho a
=> 37n + 1 chia hết cho a
Do vậy: (37n + 1) - 37n chia hết cho a
=> 1 chia hết cho a
=> a là ước của 1
=> a = 1
=> 37n + 1 và n là hai số nguyên tố cùng nhau
\(\Rightarrow BCNN\left(n;37n+1\right)=\left(37n+1\right)n=37n^2+n\)
Chứng minh rằng với mọi số tự nhiên n khác 0 thì các phân số sau là phân số tối giản n+1/n
Gọi d=ƯCLN(n+1;n)
=>\(\left\{{}\begin{matrix}n+1⋮d\\n⋮d\end{matrix}\right.\)
=>\(n+1-n⋮d\)
=>\(1⋮d\)
=>d=1
=>ƯCLN(n+1;n)=1
=>\(\dfrac{n+1}{n}\) là phân số tối giản
Đúng 0
Bình luận (0)
a,Chứng minh rằng với mọi số tự nhiên n khác 0 ta luôn có:
1²+2²+3²+...+n²=n.(n+1).(2n+1)/6
b,Chứng minh rằng
A=1.5+2.6+3.7+...+2023.2027
chia hết các số 11;23 và 2023
c,Tìm tất cả các số tự nhiên n (1 ≤ n ≤ 2000) để biểu thức B=1.3+2.3+...+n.(n+2) chia hết cho 2027