tìm tất cả các giá trị thực của m để phương trình 5sinx - 2m+1=0 có nghiệm trên (0 ; 7pi/6)
help pls :(
Tìm tất cả các giá trị thực của tham số m để phương trình cos 2 x - 2 m + 1 cos x + m + 1 = 0 có nghiệm trên khoảng π 2 ; 3 π 2 ?
A. - 1 ≤ m < 0
B. - 1 < m < 0
C. - 1 ≤ m ≤ 0
D. - 1 ≤ m < 1 2
Tìm tất cả các giá trị thực của tham số m để phương trình cos 2 x - 2 m + 1 cos x + m + 1 = 0 có nghiệm trên khoảng π 2 ; 3 π 2
![]()
![]()
![]()
![]()
Tìm tất cả giá trị thực của tham số m để phương trình cos 2 x - 2 m + 1 cos x + m + 1 = 0 có nghiệm trên khoảng π 2 ; 3 π 2
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để bất phương trình 4 x - m . 2 x + 1 + 3 - 2 m ≤ 0 có nghiệm thực
A. m ≥ 2
B. m ≤ 3
C. m ≤ 5
D. m ≥ 1
Đáp án D

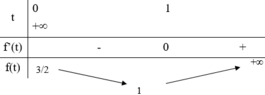
Vậy để bất phương trình có nghiệm thực thì m ≥ 1
Tìm tất cả các giá trị thực của tham số m để phương trình 2 sin 2 x − 2 m + 1 sin x + 2 m − 1 = 0 có nghiệm thuộc khoảng − π 2 ; 0 .
A. − 1 < m < 0
B. 0 < m < 1
C. 1 < m < 2
D. − 1 2 < m < 1 2
Đáp án D
Đặt t = sin x , vì x ∈ − π 2 ; 0 ⇒ t ∈ − 1 ; 0 .Khi đó, phương trình đã cho trở thành:
2 t 2 − 2 m + t t + 2 m − 1 = 0 ⇔ 2 t 2 − t − 1 − 2 m t − 1 = 0 ⇔ t − 1 2 t + 1 − 2 m = 0 ⇔ t = 2 m − 1 2 .
Mặt khác t ∈ − 1 ; 0 → − 1 < 2 m − 1 2 < 0 ⇔ − 2 < 2 m − 1 < 0 ⇔ m ∈ − 1 2 ; 1 2 .
1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)
2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)
3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm thuộc khoảng \(\left(-\dfrac{\Pi}{2};\dfrac{\Pi}{2}\right)\)
Tìm tất cả các giá trị thực của tham số m để phương trình 2 . sin 2 x - ( 2 m + 1 ) . sin x + 2 m - 1 = 0 có nghiệm thuộc khoảng - π 2 , 0 .
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để phương trình 3 x 2 - 2 m + 1 + 3 m - 5 = 0 có một nghiệm gấp ba nghiệm còn lại.
A. m = 7.
B. m = 3.
C. m = 3; m = 7.
D. m ∈ ∅.
Phương trình có hai nghiệm phân biệt ⇔ ∆ ' > 0
⇔ m 2 - 7 m + 16 > 0 ⇔ m − 7 2 2 + 15 4 > 0 , ∀ m ∈ R
Theo định lí Viet, ta có:
x 1 . x 2 = 3 m − 5 3 ; x 1 + x 2 = 2 ( m + 1 ) 3 x 1 = 3 x 2 ⇔ x 1 = m + 1 2 , x 2 = m + 1 6 x 1 . x 2 = 3 m − 5 3
⇒ m + 1 2 12 = 3 m − 5 3 ⇔ m 2 − 10 m + 21 = 0 ⇔ m = 3 m = 7
Đáp án cần chọn là: C
Tìm tất cả các giá trị thực của tham số m để phương trình x 3 - 3 x + 2 m = 0 có ba nghiệm thực phân biệt
A. m ∈ - 2 ; 2
B. - 1 ; 1
C. - ∞ ; - 1 ∪ 1 ; + ∞
D. - 2 ; + ∞