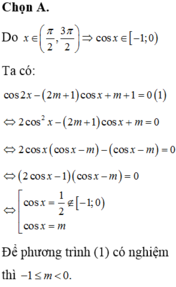Các câu hỏi tương tự
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4cos^3 x - cos 2x + (m-3)cos x - 1 = 0 có đúng 4 nghiệm khác nhau thuộc khoảng (-π/2; π/2)
Xem chi tiết
Tìm tất cả các giá trị của m để phương trình sin2x+m√2*sin(x+π/4)=0 có nghiệm.
Tìm tất cả các giá trị thực của tham số m để phương trình
2
.
sin
2
x
-
(
2
m
+
1
)
.
sin
x
+
2
m
-
1
0
có nghiệm thuộc khoảng
-
π...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 . sin 2 x - ( 2 m + 1 ) . sin x + 2 m - 1 = 0 có nghiệm thuộc khoảng - π 2 , 0 .
Tìm tất cả các giá trị của tham số m để phương trình
cos
4
x
cos
2
3
x
+
m
.
sin
2
x
có nghiệm
x
∈
0
,
π
12
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình cos 4 x = cos 2 3 x + m . sin 2 x có nghiệm x ∈ 0 , π 12
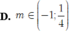
Tìm tất cả các giá trị thực của tham số m để phương trình msin^2(x) - 3cosxsinx - m - 1 = 0 có đúng 3 nghiệm thuộc khoảng (0; 3pi/2).
Có bao nhiêu giá trị nguyên của tham số m để phương trình
sin
2
x
+
cos
2
x
+
|
sin
x
+
cos
x
|
-
cos
2
x
+
m
-
m
0
có nghiệm thực? A. 9 B. 2 C. 3 D. 5
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin 2 x + cos 2 x + | sin x + cos x | - cos 2 x + m - m = 0 có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Số nghiệm của phương trình
sin
x
.
sin
2
x
+
2
.
sin
x
.
cos
2...
Đọc tiếp
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Tìm tất cả các giá trị thực của tham số m để phương trình
cos
2
x
-
2
m
+
1
cos
x
+
m
+
1
0
có nghiệm trên khoảng
π
2
;
3
π
2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình cos 2 x - 2 m + 1 cos x + m + 1 = 0 có nghiệm trên khoảng π 2 ; 3 π 2
1. Chứng minh phương trình x4 + (m2-m)x3 +mx2 - 2mx -2 0 luôn có nghiệm thuộc khoảng (0;2) với mọi giá trị của tham số m.2. Cho hàm số y dfrac{x+1}{x-1} có đồ thị (C). Tìm tất cả giá trị của tham số m để đường thẳng (d): y 2x + m cắt (C) tại hai điểm phân biệt mà hai tiếp tuyến của (C) tại hai điểm đó song song với nhau.3. Chứng minh rằng với mọi giá trị của tham số m thì phương trình x^4+mx^3-4x^2-mx+10 luôn có nghiệm trên khoảng (0;1).4. Cho hàm số: y dfrac{1}{3}x^3-left(m+1right)x^2+left...
Đọc tiếp
1. Chứng minh phương trình x4 + (m2-m)x3 +mx2 - 2mx -2 = 0 luôn có nghiệm thuộc khoảng (0;2) với mọi giá trị của tham số m.
2. Cho hàm số y = \(\dfrac{x+1}{x-1}\) có đồ thị (C). Tìm tất cả giá trị của tham số m để đường thẳng (d): y = 2x + m cắt (C) tại hai điểm phân biệt mà hai tiếp tuyến của (C) tại hai điểm đó song song với nhau.
3. Chứng minh rằng với mọi giá trị của tham số m thì phương trình \(x^4+mx^3-4x^2-mx+1=0\) luôn có nghiệm trên khoảng (0;1).
4. Cho hàm số: y = \(\dfrac{1}{3}x^3-\left(m+1\right)x^2+\left(2m+4\right)x-3\) có đồ thị (Cm) (với m là tham số). Tìm m để trên đồ thị (Cm) có hai điểm phân biệt có hoành độ cùng dấu và tiếp tuyến của (Cm) tại mỗi điểm đó vuông góc với đường thẳng d: \(x+3y-6=0\)
5. Cho hàm số y = \(\dfrac{x+1}{x-2}\) có đồ thị (C); đường tròn (T) có tâm I(2;-5) và đi qua điểm E(3;-1). Tìm toạ độ các điểm M thuộc đồ thị (C) để tiếp tuyến của (C) tại M cắt đường tròn (T) tại hai điểm A, B sao cho tam giác EAB vuông tại E.