1. Cho tam giác ABC vuông tại A, đường cao AH gọi MN là chân các đường vuông góc kẻ từ H đến AB và AC.
a) CMR AMHN là HCN
b) Gọi P là trung điểm của HC, CMR tam giác MNP vuông
c) Tam giác ABC cần điều kiện gì để MN=2NP
mn giúp e
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E lần lượt là chân đường vuông góc kẻ từ H đến AB, AC.
a) CM: AH= DE
b) Gọi I là trung diểm HB, K là trung điểm HC. CMR: DI//EK
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
hay AH=DE
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH =12cm; BC = 18cm
Bài 2: Cho tam giác ABC (AC > AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:
a, DE là đường trung trực của AH
b, DEKH là hình thang cân
Bài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.
a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AH
b, CM: AI vuông góc với BD
Cho tam giác ABC vuông ở A, đường cao AH. Gọi D, E lần lượt là chân đường vuông góc kẻ từ H đến AB, AC; O là giao điểm của AH và DE .
Gọi I, K theo thứ tự là trung điểm của HB, HC. Chứng minh tam giác IDO = tam giác IHO
Giúp mik với đang cần gấp:((
Xét tứ giác AEHD, có:
∠A = ∠E = ∠D = 90°
=> tứ giác AEHD là hình chữ nhật.
O là giao điểm hai đường chéo hcn AEHD
=> OD = OH (1).
DI là đường trung tuyến ứng với cạnh huyền của Δ vuông DHB
=> DI = 1/2 BH = IH (2).
Xét Δ IDO và Δ IHO, có:
OD = OH (1).
OI là cạnh chung.
DI = IH (2).
=> Δ IDO = Δ IHO (đpcm).
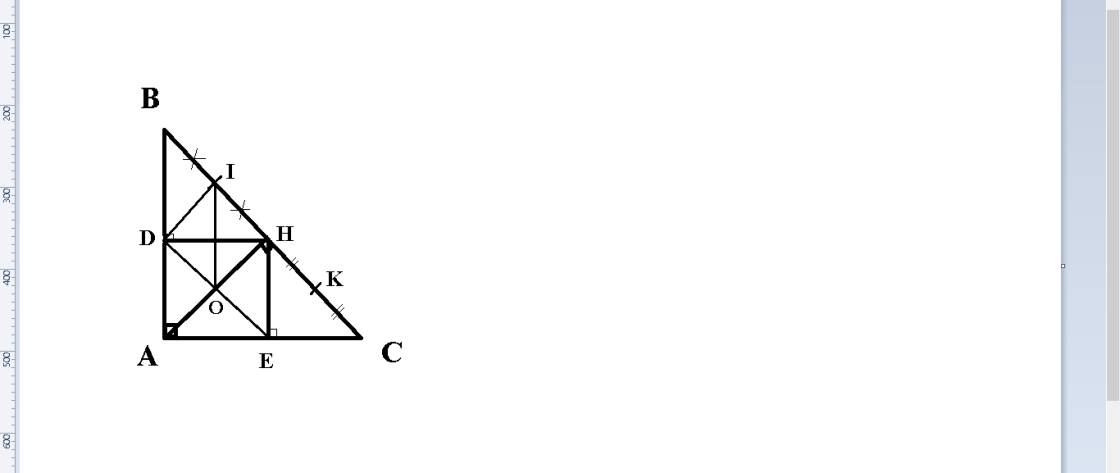
(bồ xem thử ổn hông nhe).
cho tam giác ABC vuông tại A ,đường cao AH. kẻ HM vuông góc AB ,HN vuông góc với AC .MN giao AH tại O
cho AMHN là hình chữ nhật , các điểm A,M,N,H cách đều 1 điểm .gọi K là trung điểm HC .cmBO vuông góc với AK
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{NAM}=90^0\)
Do đó: AMHN là hình chữ nhật
cho tam giác ABC vuông tại A đg cao AH (H thuộc BC) . M và N lần lượt là chân đg vuông góc kẻ từ H đến AB và AC
a) CMR: HM=AN
b) AH=MN
c) gọi i là dao điểm của AH và MN .CMR : IM=IN
d) nếu tam giác ABC là tam giác cân . CMR: MN sog sog BC
mình cần gấp . giúp mik vs
HM _|_ AB (gt)
AB _|_ AC do tam giác ABC vuông tại A (gt)
AN; HM phân biệt
=> AN // HM (tc)
=> góc NAH = góc AHM (slt)
xét tam giác NAH và tam giác MHA có : AH chung
góc ANH = góc AMH = 90
=> tam giác NAH = tam giác MHA (ch-gn)
=> HM = AN (đn)
b, NA = HM (câu a)
xét tam giác NAM và tam giác HMA có : AM chung
góc NAM = góc HMA = 90
=> tam giác NAM = tam giác HMA (2cgv)
=> AH = MN (đn)
c, AN // HM (câu a)
=> góc NAH = góc AHM (slt) và góc ANM = góc NMH (slt)
xét tam giác NAI và tam giác MHI có : AN = MH (câu a)
=> tam giác NAI = tam giác MHI (g-c-g)
=> NI = IM (đn)
d,
cho tam giác ABC vuông ở A, AH là đường cao, kẻ HN vuông góc AB, HM vuông góc AC. Gọi O trung điểm MN. Từ A kẻ Ax vuông góc BO tại K và Ax cắt BC tại I. Cmr: I là trung điểm HC
Cho tam giác ABC vuông tại A, đường cao AH . Gọi M,N theo thứ tự là các chân đường vuông góc kéo dài từ H đến AB, AC .
Gọi O là giao điểm của AH và MN ; K là trung điểm của CH .
a) Cm: Tứ giác AMHN là hình chư nhật
b) Tính góc MNK.
c) Cm: BO vuông góc AK
Cho tam giác ABC cân tại A, đường cao AH. Gọi M là trung điểm của AH, K là chân đường vuông góc kẻ từ H đến CM. CMR góc AKB vuông
Cho tam giác ABC vuông tại A , đường cao AH . Gọi D , E theo thứ tự là chân các đường vuông góc kẻ từ H xuống AB và AC .
a, Tứ giác ADHE là hình gì ? Vì sao ?
b, Gọi M là trung điểm của HC . Chứng minh tam giác DEM vuông .
c, Tam giác ABC cần có thêm điều kiện gì để DE = 2.EM