Tọa độ giao điểm của đồ thị các hàm số:
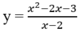
và y = x + 1 là:
A. (2; 2); B. (2; -3);
C(-1; 0); D. (3; 1).
1) Trên cùng 1 mặt phẳng tọa độ hãy vẽ đồ thị các hàm số sau ; y=3x và y=x+2 2) tìm tọa độ giao điểm của đồ thị 3 hàm số vừa vẽ ở câu 1
2. PT hoành độ giao điểm: \(3x=x+2\Leftrightarrow2x=2\Leftrightarrow x=1\Leftrightarrow y=3\Leftrightarrow A\left(1;3\right)\)
Vậy \(A\left(1;3\right)\) là giao 2 đths
cho hàm số : y=x\(^2\)và y=-2x+3
a) vẽ đồ thị của hàm số trên cùng mặt phẳng tọa độ Oxy.
b) tìm tọa độ các giao điểm của hai đồ thị trên
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2=-2x+3\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+2x-3=0\\y=x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+3\right)\left(x-1\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(-3;9\right);\left(1;1\right)\right\}\)
Cho hàm số y=x² ; y=2x+3 a, vẽ các đồ thị trên cùng 1 mặt phẳng tọa độ b, tìm hoành độ giao điểm chung của 2 đồ thị
b: Hoành độ giao điểm chung là:
\(x^2-2x-3=0\)
=>(x-3)(x+1)=0
=>x=3 hoặc x=-1
a. Cho hai hàm số y = x^2 có đồ thị (P) và y = x + 2 có đồ thị (D). trùng
Vẽ (P) và (D) trên cùng một trục hệ tọa độ vuông góc Oxy. Xác định tọa độ tại các giao điểm của chúng
b. Cho hàm số y = (m - 1)x + m + n . Tính giá trị của m,n để đồ thị hàm số trùng với đồ thị hàm số y = -2x + 1
a: 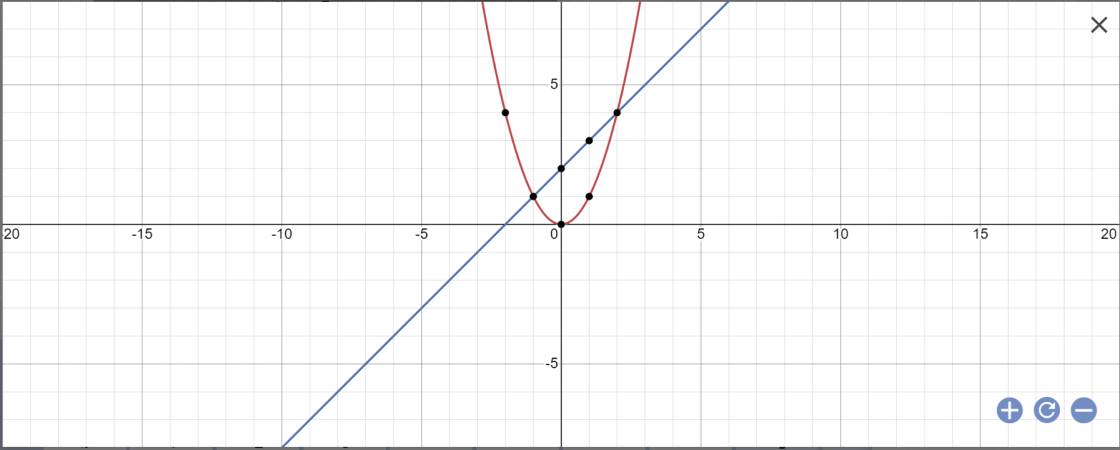
PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
Khi x=-1 thì y=(-1)^2=1
Khi x=2 thì y=2^2=4
b: Để y=(m-1)x+m+n trùng với y=-2x+1 thì
m-1=-2 và m+n=1
=>m=-1 và n=1-m=1-(-1)=2
Cho các hàm số sau : y = 2x + 1 và y = x - 3
a) Vẽ đồ thị của các hàm số trên cùng một mặt phẳng tọa độ
b) Gọi M là giao điểm của hai đồ thị trên . Tìm tọa độ điểm M
Lời giải:
a.
Đồ thị xanh lá: $y=2x+1$
Đồ thị xanh dương: $y=x-3$
b.
PT hoành độ giao điểm:
$y=2x+1=x-3$
$\Leftrightarrow x=-4$
$y=x-3=(-4)-3=-7$
Vậy tọa độ điểm $M$ là $(-4;-7)$
cho hàm số \(y=x^2-3x+2\) có đồ thị (P)
a.tìm tọa độ giao điểm của (P) với Ox
b.tìm tọa độ giao điểm của (P) với Oy
c.tìm tọa độ giao điểm của (P) với đường thẳng y = x-1
a: Đặt y=0
=>\(x^2-3x+2=0\)
=>\(x^2-x-2x+2=0\)
=>\(x\cdot\left(x-1\right)-2\left(x-1\right)=0\)
=>(x-1)(x-2)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Vậy: Tọa độ giao điểm của (P) với trục Ox là A(1;0) và B(2;0)
b: Thay x=0 vào (P), ta được:
\(y=0^2-3\cdot0+2=2\)
Vậy: (P) cắt trục Oy tại điểm C(0;2)
c: Phương trình hoành độ giao điểm là:
\(x^2-3x+2=x-1\)
=>\(x^2-3x+2-x+1=0\)
=>\(x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
Khi x=1 thì \(y=1-1=0\)
Khi x=3 thì y=3-1=2
Vậy: Tọa độ giao điểm của (P) với đường thẳng y=x-1 là D(1;0) và E(3;2)
Lời giải:
a. Gọi giao điểm của $(P)$ với $Ox$ là $A$. Vì $A\in Ox$ nên $y_A=0$
$A\in (P)$ nên $y_A=x_A^2-3x_A+2$
$\Leftrightarrow 0=x_A^2-3x_A+2$
$\Leftrightarrow (x_A-1)(x_A-2)=0$
$\Leftrightarrow x_A=1$ hoặc $x_A=2$
$\Rightarrow$ tọa độ: $(2,0), (1,0)$
b.
Gọi $B$ là giao điểm của $(P)$ với $Oy$
$B\in Oy$ nên $x_B=0$
$y_B=x_B^2-3x_B+2=2$
Vậy giao điểm là $(0,2)$
c.
PT hoành độ giao điểm:
$x^2-3x+2=x-1$
$\Leftrightarrow x^2-4x+3=0$
$\Leftrightarrow (x-1)(x-3)=0$
$\Leftrightarrow x=1$ hoặc $x=3$
Nếu $x=1$ thì $y=x-1=1-1=0$
Nếu $x=3$ thì $y=x-1=3-1=2$
Vậy 2 giao điểm là: $(1,0), (3,2)$
Cho hàm số (d): y=2x+3. a, Vẽ đồ thị của hàm số đã cho. b, Tìm tọa độ giao điểm của (d) với hai trục tọa độ. c) Trong các điểm sau, điểm nào thuộc đồ thị hàm số, điểm nào không thuộc đồ thị hàm số: A( -1; 1) B( 2; 3) C(1/2;4)
Vẽ đồ thị hai hàm số y=-x+5 và y=2x-2 trên cùng 1 mặt phẳng tọa độ
Tìm tọa độ giao điểm của 2 đồ thị trên
Phương trình hoành độ giao điểm:
\(-x+5=2x-2\Leftrightarrow x=\dfrac{7}{3}\Rightarrow y=\dfrac{8}{3}\Rightarrow\left(\dfrac{7}{3};\dfrac{8}{3}\right)\)
\(a,\) Hàm số: \(y=-x+5\)
Lấy: \(\left\{{}\begin{matrix}x=1\Rightarrow y=4\\x=2\Rightarrow y=3\end{matrix}\right.\)
Hàm số: \(y=2x-2\)
\(\left\{{}\begin{matrix}x=2\Rightarrow y=2\\x=3\Rightarrow y=4\end{matrix}\right.\)

\(b,\left\{{}\begin{matrix}y=-x+5\left(d\right)\\y=2x-2\left(d'\right)\end{matrix}\right.\)
Phương trình hoành độ giao điểm của \(\left(d\right)\) và \(\left(d'\right)\) là:
\(-x+5=2x-2\)
\(\Leftrightarrow-3x=-7\)
\(\Leftrightarrow x=\dfrac{7}{3}\)
Thay \(x=\dfrac{7}{3}\) vào \(\left(d\right)y=-x+5\) ta được:
\(y=-\dfrac{7}{3}+5\)
\(\Leftrightarrow y=\dfrac{8}{3}\)
Vậy tọa độ giao điểm của hai đường thẳng là \(B\left(\dfrac{7}{3};\dfrac{8}{3}\right)\)
không vẽ đồ thị hãy tìm tọa độ các giao điểm của các đồ thị hàm số sau:
a) y=x\(^2\)và y=\(\dfrac{1}{2}\)x b) y=\(-\dfrac{1}{2}x^2\)và y=mx+\(\dfrac{1}{2}m^2-8\)
a, Hoành độ giao điểm tm pt
\(x^2-\dfrac{1}{2}x=0\Leftrightarrow x\left(x-\dfrac{1}{2}\right)=0\Leftrightarrow x=0;x=\dfrac{1}{2}\)
Với x = 0 => y = 0
Với x = 1/2 => y = 1/4
Vậy (P) cắt (d) tại O(0;0) ; A(1/2;1/4)
Cho hai hàm số y = 1 3 x 2 và y = -x + 6.
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị đó.
a)
- Vẽ đường thẳng y = -x + 6
Cho x = 0 ⇒ y = 6 được điểm (0, 6)
Cho y = 0 ⇒ x = 6 được điểm (6, 0)
⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).
- Lập bảng giá trị và vẽ đồ thị hàm số 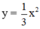
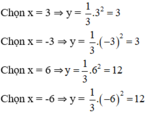
⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).
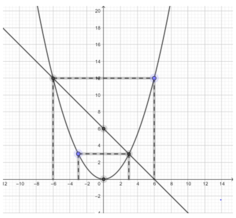
b)Xét phương trình hoành độ giao điểm
