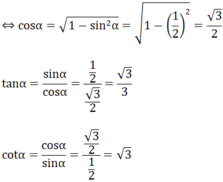Cho tanα - 3cotα = 6 và π < α < 3π/2. Tính
sinα + cosα
Cho tanα - 3cotα = 6 và π < α < 3π/2. Tính
![]()
Cho cos α=-2/5 và π<α<3π/2. tính tanα, sinα ,cotα
\(sin\alpha=-\sqrt{1-cos^2\alpha}=-\dfrac{\sqrt{21}}{5}\)
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\dfrac{\sqrt{21}}{5}}{-\dfrac{2}{5}}=\dfrac{\sqrt{21}}{2}\)
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{2}{\sqrt{21}}\)
Cho tanα = 2cotα và 3π/2 < α < 2π. Giá trị của biểu thức sinα + cosα là

Vì tanα = 2cotα và 3π/2 < α < 2π nên 3π/2 < α < 7π/4.
Do đó sinα < (- 2 )/2 và cosα < 2 /2.
Vì vậy sinα + cosα < 0.
Suy ra các phương án A, C, D bị loại.
Đáp án: B
a) Cho cos α = 2 3 . Tính giá trị của biểu thức
A = tan α + 3 c o t α tan α + c o t α
b) Cho sin α = 3 5 v à 90 ° < α < 180 °
Tính giá trị của biểu thức:
C = c o t α - 2 tan α tan α + 3 c o t α
Cho góc α thỏa mãn sin2α = -4 / 5 và 3π / 4 < α < π. Tính P = sinα - cosα.
3/4pi<a<pi
=>sin a>0; cosa<0
sin2a=-4/5
=>2*sina*cosa=-4/5
=>sina*cosa=-2/5
(sina-cosa)^2=sin^2a+cos^2a-2*sina*cosa=1+4/5=9/5
=>sin a-cosa=3/căn 5
Cho góc α thỏa mãn tanα = 2 và 1800< α< 2700 . Tính P = cosα + sinα
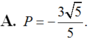
![]()

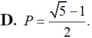
Cho A B C ^ = 60 0 và ∆ABC tam giác nhọn
a, Tính sinα, tanα, cotα, biết cosα = 1 5
b, Tính cosα, tanα, cotα, biết sinα = 2 3
c, Cho tanα = 2. Tính sinα, cosα, cotα
d, Cho cotα = 3. Tính sinα, cosα, tanα
a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Cho α là góc nhọn, sinα = 1/2.Tính cosα;tanα;cotα
Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1