Gọi α là mặt phẳng đi qua M 1 ; − 1 ; 2 và chứa trục Ox. Điểm nào trong các điểm sau đây thuộc mặt phẳng α ?
A. M 0 ; 4 ; − 2 .
B. N 2 ; 2 ; − 4 .
C. P − 2 ; 2 ; 4 .
D. Q 0 ; 4 ; 2 .
Những câu hỏi liên quan
Cho mặt phẳng
(
α
)
đi qua M(1;
-
3;4) và song song với mặt phẳng
(
β
)
: 6x – 5y +z – 7 0. Phương trình mặt phẳng
(
α
)
là: A. 6x
-
5y + z + 25 0 B. 6x
-
5y + z
-
25 0 C. 6x ...
Đọc tiếp
Cho mặt phẳng ( α ) đi qua M(1; - 3;4) và song song với mặt phẳng ( β ) : 6x – 5y +z – 7 = 0. Phương trình mặt phẳng ( α ) là:
A. 6x - 5y + z + 25 = 0
B. 6x - 5y + z - 25 = 0
C. 6x - 5y + z - 7 = 0
D. 6x - 5y + z + 17 = 0
Đáp án B.
Phương pháp: Mặt phẳng ( α ) đi qua M(1; - 3;4) và nhận n β → = 6 ; - 5 ; 1 là 1 VTPT.
Cách giải: Mặt phẳng ( α ) đi qua M(1; - 3;4) và nhận n β → = 6 ; - 5 ; 1 là 1 VTPT nên có phương trình:
6(x - 1) - 5(y+3)+(z - 4)=0
→ 6x - 5y + z - 25 = 0
Đúng 0
Bình luận (0)
Cho mặt phẳng
α
đi qua M(1;-3;4) và song song với mặt phẳng
β
: 6x -5y+z-70. Phương trình mặt phẳng
α
là: A. 6x-5y+z+250 B. 6x-5y+z-250 C. 6x-5y+z-70 D. 6x-5y+z+170
Đọc tiếp
Cho mặt phẳng α đi qua M(1;-3;4) và song song với mặt phẳng β : 6x -5y+z-7=0. Phương trình mặt phẳng α là:
A. 6x-5y+z+25=0
B. 6x-5y+z-25=0
C. 6x-5y+z-7=0
D. 6x-5y+z+17=0
Đáp án B.
Phương pháp: Mặt phẳng α đi qua M và nhận
Cách giải: Mặt phẳng α đi qua M và nhận là 1 VTPT nên có phương trình:
nên có phương trình:
Đúng 0
Bình luận (0)
Cho mặt phẳng
α
đi qua M(1;-3;4) và song song với mặt phẳng
β
: 6x +2y-z-70. Phương trình mặt phẳng
α
là: A. 6x +2y-z+80. B. 6x +2y-z+40. C. 6x +2y-z-40. D. 6x +2y-z-170.
Đọc tiếp
Cho mặt phẳng α đi qua M(1;-3;4) và song song với mặt phẳng β : 6x +2y-z-7=0. Phương trình mặt phẳng α là:
A. 6x +2y-z+8=0.
B. 6x +2y-z+4=0.
C. 6x +2y-z-4=0.
D. 6x +2y-z-17=0.
Đáp án B.
Phương pháp: Mặt phẳng α đi qua M
Cách giải: Mặt phẳng α đi qua M và
nên có phương trình:
Đúng 0
Bình luận (0)
Cho mặt phẳng
(
α
)
đi qua điểm M(1; –3;4) và song song với mặt phẳng
(
β
)
: 6x + 2y – z – 7 0. Phương trình mặt phẳng
(
α
)
là : A. 6x + 2y – z +8 0 B. 6x + 2y – z +4 0 C. 6x + 2y – z – 4 0 D. 6x + 2y – z – 17 0
Đọc tiếp
Cho mặt phẳng ( α ) đi qua điểm M(1; –3;4) và song song với mặt phẳng ( β ) : 6x + 2y – z – 7 = 0. Phương trình mặt phẳng ( α ) là :
A. 6x + 2y – z +8 = 0
B. 6x + 2y – z +4 = 0
C. 6x + 2y – z – 4 = 0
D. 6x + 2y – z – 17 = 0
Đáp án B.
Phương pháp: Mặt phẳng ( α ) đi qua M(1; –3;4) và nhận n ( β ) → = ( 6 ; 2 - 1 ) là 1 VTPT.
Cách giải: Mặt phẳng ( α ) đi qua M(1; –3;4) và nhận n ( β ) → = ( 6 ; 2 - 1 ) là 1 VTPT nên có phương trình:
6(x– 1) + 2(y+3) – (z– 4) = 0 → 6x + 2y – z +4 = 0
Đúng 0
Bình luận (0)
Cho mặt phẳng
α
đi qua M(1;-3;4) và song song với mặt phẳng
β
: 6x-5y+z-70. Phương trình của mặt phẳng
α
là:
Đọc tiếp
Cho mặt phẳng α đi qua M(1;-3;4) và song song với mặt phẳng β : 6x-5y+z-7=0. Phương trình của mặt phẳng α là:
Cho hình chóp S.ABC. Gọi
α
là mặt phẳng đi qua A và song song với BC. Mặt phẳng
α
cắt SB, SC lần lượt tại M, N. Tính tỉ số
S
M
S
B
biết
α
chia khối chóp thành 2 phần có thể tích bằng nhau A. 1/2 C. 1/3
Đọc tiếp
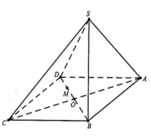
Cho hình chóp S.ABC. Gọi α là mặt phẳng đi qua A và song song với BC. Mặt phẳng α cắt SB, SC lần lượt tại M, N. Tính tỉ số S M S B biết α chia khối chóp thành 2 phần có thể tích bằng nhau
A. 1/2
C. 1/3
Trong không gian với hệ tọa độ Oxyz cho hai điểm P(2;0;-1), Q(1;-1;3) và mặt phẳng
P
:
3
x
+
2
y
-
z
+
5
0
. Gọi
α
là mặt phẳng đi qua P, Q và vuông góc với (P), phương trình của mặt phẳng
α
là A.
α
: -7x + 11y + z - 3 0 B.
α
: 7x - 11y + z - 1 0 C...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai điểm P(2;0;-1), Q(1;-1;3) và mặt phẳng P : 3 x + 2 y - z + 5 = 0 . Gọi α là mặt phẳng đi qua P, Q và vuông góc với (P), phương trình của mặt phẳng α là
A. α : -7x + 11y + z - 3 = 0
B. α : 7x - 11y + z - 1 = 0
C. α : -7x + 11y + z + 15 = 0
D. α : 7x - 11y - z + 1 = 0
Ta có 
mặt phẳng (P) có VTPT 
Suy ra 
Mặt phẳng
α
đi qua P(2;0;-1) và nhận 
làm một VTPT nên có phương trình
α
: -7x + 11y + z + 15 = 0
Chọn C.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông. Gọi O là giao điểm của AC và BD, M là trung điểm của DO,
α
là mặt phẳng đi qua M và song song với AC và SD. Tiết diện của hình chóp cắt bởi mặt phẳng
α
là hình gì? A. Ngũ giác B. Tứ giác C. Lục giác D. Tam giác
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông. Gọi O là giao điểm của AC và BD, M là trung điểm của DO, α là mặt phẳng đi qua M và song song với AC và SD. Tiết diện của hình chóp cắt bởi mặt phẳng α là hình gì?
A. Ngũ giác
B. Tứ giác
C. Lục giác
D. Tam giác
Cho hình chóp
S
.
A
B
C
có M là điểm di động trên cạnh SA sao cho
S
M
S
A
k
. Gọi (α) là mặt phẳng đi qua M và song song với mặt phẳng
A
B
C
. Tìm k để mặt phẳng (α) cắt hình chóp
S
.
A
B
C
theo mộ...
Đọc tiếp
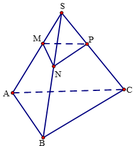
Cho hình chóp S . A B C có M là điểm di động trên cạnh SA sao cho S M S A = k . Gọi (α) là mặt phẳng đi qua M và song song với mặt phẳng A B C . Tìm k để mặt phẳng (α) cắt hình chóp S . A B C theo một thiết diện có diện tích bằng một nửa diện tích tam giác ABC.
A. k = 2 2 .
B. k = 1 2 .
C. k = 3 2 .
D. k = 1 3 .
Đáp án A
Gọi N, P là hai điểm lần lượt thuộc S B , S C thỏa mãn M N / / A B , M P / / A C .
Ta có M N // A B ⇒ M N // A B C M P // A C ⇒ M P // A B C ⇒ M N P / / A B C .
Gọi h 1 là đường cao của ΔMNP ứng với đáy MN.
Gọi h 2 là đường cao của ΔABC ứng với đáy AB.
Dễ thầy ΔMNP đồng dạng ΔABC ta có M N A B = h 1 h 2 = k .
Vậy để thỏa mãn yêu cầu bài toán
S Δ M N P S Δ A B C = 1 2 h 1 . M N 1 2 h 2 . A B = 1 2 ⇔ k . k = 1 2 ⇔ k = 2 2
Đúng 0
Bình luận (0)