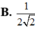Các câu hỏi tương tự
Cho hình chóp S.ABC có đáy là
Δ
A
B
C
vuông cân ở B,
A
C
a
2
,
S
A
a
và
S
A
⊥
A
B
C
. Gọi G là trọng tâm
Δ
S
B
C
, một mặt phẳng
α
đi qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Thể tích khối chóp S.AMN bằng : A. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy là Δ A B C vuông cân ở B, A C = a 2 , S A = a và S A ⊥ A B C . Gọi G là trọng tâm Δ S B C , một mặt phẳng α đi qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Thể tích khối chóp S.AMN bằng :
A. 4 a 3 27
B. 2 a 3 9
C. 4 a 3 9
D. 2 a 3 27
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B,
A
C
a
2
,
S
A
⊥
m
p
A
B
C
,
S
A
a
. Gọi G là trọng tâm tam giác SBC, mặt phẳng (α) đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN A.
V
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, A C = a 2 , S A ⊥ m p A B C , S A = a . Gọi G là trọng tâm tam giác SBC, mặt phẳng (α) đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN
A. V = a 3 9
B. V = 2 a 3 27
C. V = 2 a 3 9
D. V = a 3 6
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B,
A
C
a
2
biết SA vuông góc với mặt đáy, SA a. Gọi G là trọng tâm của tam giác SBC,
α
là mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M và N. Tính thể tích V của khối đa diện AMNBC. A.
V
4
9
a
3
B.
V...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, A C = a 2 biết SA vuông góc với mặt đáy, SA = a. Gọi G là trọng tâm của tam giác SBC, α là mặt phẳng đi qua AG và song song với BC cắt SB, SC lần lượt tại M và N. Tính thể tích V của khối đa diện AMNBC.
A. V = 4 9 a 3
B. V = 2 27 a 3
C. V = 5 27 a 3
D. V = 5 54 a 3
Cho hình chóp S.ABC, M và N là các điểm thuộc các cạnh SA và SB sao cho MA 2SM, SN 2NB,
α
là mặt phẳng qua MN và song song với SC. Kí hiệu (H1) và (H2) là các khối đa diện có được khi chia khối chóp S.ABC bới mặt phẳng
α
trong đó (
H
1
) chứa điểm S, (
H
2
) chứa điểm A;
V
1
và
V
2...
Đọc tiếp
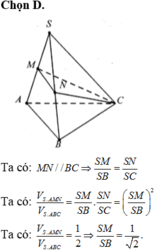
Cho hình chóp S.ABC, M và N là các điểm thuộc các cạnh SA và SB sao cho MA= 2SM, SN = 2NB, α là mặt phẳng qua MN và song song với SC. Kí hiệu (H1) và (H2) là các khối đa diện có được khi chia khối chóp S.ABC bới mặt phẳng α trong đó ( H 1 ) chứa điểm S, ( H 2 ) chứa điểm A; V 1 và V 2 lần lượt là thể tích của ( H 1 ) và ( H 2 ). Tính tỉ số V 1 V 2
A. 4/3
B. 5/4
C. 3/4
D. 4/5
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng
α
đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số
S
N
S
D
để
α
chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau. A.
1
2
B.
1
3
C.
5...
Đọc tiếp
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, mặt phẳng α đi qua AB cắt cạnh SC, SD lần lượt tại M, N. Tính tỉ số S N S D để α chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
A. 1 2
B. 1 3
C. 5 - 1 2
D. 3 - 1 2
Cho khối chóp S.ABC. Gọi G là trọng tâm của tam giác SBC. Mặt phẳng
(
α
)
qua AG và song song với BC cắt SB, SC lần lượt tại I, J. Tính tỉ số thể tích của hai khối tứ diện SAIJ và SABC A.
2
9
B.
2
3
C.
4
9
D.
8
27
Đọc tiếp
Cho khối chóp S.ABC. Gọi G là trọng tâm của tam giác SBC. Mặt phẳng ( α ) qua AG và song song với BC cắt SB, SC lần lượt tại I, J. Tính tỉ số thể tích của hai khối tứ diện SAIJ và SABC
A. 2 9
B. 2 3
C. 4 9
D. 8 27
Cho khối chóp S.ABC. Gọi G là trọng tâm của tam giác SBC. Mặt phẳng (α) qua AG và song song với BC cắt SB,SC lần lượt tại I,J. Tính tỉ số thể tích của hai khối tứ diện SAIJ và SABC. A.
1
9
. B.
4
9
. C.
1
3
. D.
2
3
.
Đọc tiếp
Cho khối chóp S.ABC. Gọi G là trọng tâm của tam giác SBC. Mặt phẳng (α) qua AG và song song với BC cắt SB,SC lần lượt tại I,J. Tính tỉ số thể tích của hai khối tứ diện SAIJ và SABC.
A. 1 9 .
B. 4 9 .
C. 1 3 .
D. 2 3 .
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K,M lần lượt là trung điểm của các đoạn thẳng SA, SB, (α) là mặt phẳng qua K song song với AC và AM. Mặt phẳng (α) chia khối chóp S.ABCD thành hai khối đa diện. Gọi
V
1
là thể tích của khối đa diện chứa đỉnh S và
V
2
là thể tích khối đa diện còn lại. Tính tỉ số
V
1
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K,M lần lượt là trung điểm của các đoạn thẳng SA, SB, (α) là mặt phẳng qua K song song với AC và AM. Mặt phẳng (α) chia khối chóp S.ABCD thành hai khối đa diện. Gọi V 1 là thể tích của khối đa diện chứa đỉnh S và V 2 là thể tích khối đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 7 25
B. V 1 V 2 = 5 11
C. V 1 V 2 = 7 17
D. V 1 V 2 = 9 23
Cho hình chóp S.ABCD. Trên cạnh SA lấy điểm M sao cho
SM
1
3
SA
. Mặt phẳng
α
qua M và song song với mặt đáy lần lượt cắt SB, SC, SD tại N, P, Q. Tỉ số thể tích của khối chóp S.MNPQ với khối chóp S.ABCD là A.
1
9
B.
1
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD. Trên cạnh SA lấy điểm M sao cho SM = 1 3 SA . Mặt phẳng α qua M và song song với mặt đáy lần lượt cắt SB, SC, SD tại N, P, Q. Tỉ số thể tích của khối chóp S.MNPQ với khối chóp S.ABCD là
A. 1 9
B. 1 3
C. 1 81
D. 1 27