Khoảng cách từ gốc tọa độ đến giao điểm của hai đường tiệm cận của đồ thị hàm số y = 2 x + 1 x + 1 bằng
A. 2 .
B. 5 .
C. 5.
D. 3 .
Trong mặt phẳng tọa độ Oxy, tổng khoảng cách từ gốc tọa độ đến tất cả các đường tiệm cận của đồ thị hàm số y = log 2 2 x + 3 x - 1 bằng

![]()
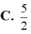
![]()
Gọi M là điểm có hoành độ dương thuộc đồ thị hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất. Tọa độ điểm M là
A. 4 ; 3
B. 0 ; − 1
C. 1 ; − 3
D. 3 ; 5
Tìm tọa độ điểm M có hoành độ dương thuộc đồ thị (C) của hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất.
A. M(1;-3)
B. M(3;5)
C. M(0;-1)
D. M(4;3)
Đáp án là D

Dấu “ = ” xảy ra ó
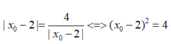
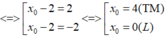
Vậy M(4;3)
Cho hàm số y = 2 x + 1 x - 1 có đồ thị (C) . Gọi I là giao điểm của hai tiệm cận. Tiếp tuyến của (C) cắt 2 tiệm cận tại A và B sao cho chu vi tam giác IAB đạt giá trị nhỏ nhất. Khoảng cách lớn nhất từ gốc tọa độ đến tiếp tuyến ∆ gần giá trị nào nhất?
A. 6.
B. 4.
C. 3.
D. 5.
+ Gọi M ( x 0 ; 2 + 3 x 0 - 1 ) ∈ C , x 0 ≠ 1 .
Phương trình tiếp tuyến tại M có dạng
∆ : y = - 3 x 0 - 1 2 ( x - x 0 ) + 2 + 3 x 0 - 1
+ Giao điểm của ∆ với tiệm cận đứng là A ( 1 ; 2 + 6 x 0 - 1 )
+ Giao điểm của ∆ với tiệm cận ngang là B( 2x0-1; 2).
Ta có S ∆ I A B = 1 2 I A . I B = 1 2 . 6 x 0 - 1 . 2 . x 0 - 1 = 2 . 3 = 6
Tam giác IAB vuông tại I có diện tích không đổi nên chu vi tam giác IAB đạt giá trị nhỏ nhất khi
IA=IB 
+Với x 0 = 1 + 3 thì phương trình tiếp tuyến là ∆ : y = - x + 3 + 2 3 . Suy ra
d O , ∆ = 3 + 2 3 2
+ Với x 0 = 1 - 3 thì phương trình tiếp tuyến là ∆ : y = - x + 3 - 2 3 . Suy ra
d O , ∆ = - 3 + 2 3 2
Vậy khoảng cách lớn nhất là 3 + 2 3 2 gần với giá trị 5 nhất trong các đáp án.
Chọn D.
Tọa độ các điểm thuộc đồ thị (C) của hàm số y = 2 x + 1 x - 1 mà có tổng khoảng cách đến hai đường tiệm cận của (C) bằng 4 là
A.![]()
B. ![]()
C.![]()
D. ![]()
Đáp án C
Gọi 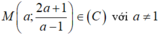 với
a
≢
1
.
với
a
≢
1
.
Tiệm cận đừng và tiệm cận ngang của (C) lần lượt có phương trình
![]() .
.
Khoảng cách từ M đến tiệm cận đứng là
![]()
Khoảng cách từ M đến tiệm cận ngang là
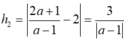
Tổng khoảng cách từ M đến hai đường tiệm cận bằng 4 nên ta có:
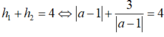 .
.
![]()
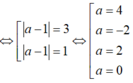
Vậy các điểm cần tìm là: ![]() .
.
Tọa độ điểm M có hoành độ dương thuộc đồ thị hàm số y = x + 2 x - 2 sao cho tổng khoảng cách từ M đến 2 tiệm cận của đồ thị hàm số đạt giá trị nhỏ nhất là
A.![]()
B. ![]()
C.![]()
D.![]()
Cho hàm số có đồ thị y = x − 2 x + 2 có đồ thị (C). Tìm tọa độ giao điểm I của hai đường tiệm cận của đồ thị (C)
A. I(-2;2)
B. I(-2;2)
C. I(2;1)
D. I(-2;1)
Cho đồ thị (C) của hàm số y = 2 x + 2 x − 1 . Tọa độ điểm M nằm trên (C) sao cho tổng khoảng cách từ M đến hai tiệm cận của (C) nhỏ nhất là
A. M − 1 ; 0 M 3 ; 4
B. M − 1 ; 0 M 0 ; − 2
C. M 2 ; 6 M 3 ; 4
D. M 0 ; − 2 M 2 ; 6
Đáp án A
Gọi M a ; 2 a + 2 a − 1 , tiệm cận đứng x = 1 ; tiệm cận ngang y = 2 .
Khi đó d = d M ; T C D + d M ; T C N = a − 1 + 4 a − 1 ≥ 4
Dấu bằng xảy ra ⇔ a − 1 2 = 4 ⇔ a = 3 a = − 1 ⇒ M − 1 ; 0 M 3 ; 4 .
Cho đồ thị (C) của hàm số y = 2 x + 2 x − 1 . Tọa độ điểm M nằm trên (C) sao cho tổng khoảng cách từ M đến hai tiệm cận của (C) nhỏ nhất là
A. M − 1 ; 0 M 3 ; 4
B. M − 1 ; 0 M 0 ; − 2
C. M 2 ; 6 M 3 ; 4
D. M 0 ; − 2 M 2 ; 6
Đáp án A
Đồ thị hàm số y = 2 x + 2 x − 1 C có hai đường tiệm cận là x = 1 d 1 ; y = 2 d 2 .
Gọi M ∈ C ⇒ M m ; 2 m + 2 m − 1 → d M ; d 1 = m − 1 d M ; d 2 = 2 m + 2 m − 1 − 2 = 4 m − 1
Khi đó d M ; d 1 + d M ; d 2 = m − 1 + 4 m − 1 ≥ 2 m − 1 . 4 m − 1 = 4 .
Dấu “=” xảy ra ⇔ m − 1 = 4 m − 1 ⇔ m − 1 2 = 4 ⇔ m = 3 m = − 1 .
Vậy M 3 ; 4 M − 1 ; 0 .