Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a 2 , S A = 2 a . Côsin của góc giữa (SDC) và (SAC) bằng:
A. 21 14
B. 21 3
C. 21 2
D. 21 7
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a 2 , S A = 2 a . Côsin của góc giữa (SDC) và (SAC) bằng:
A. 21 14
B. 21 3
C. 21 2
D. 21 7
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết rằng côsin của góc giữa (SCD) và (ABCD) bằng 2 19 19 . Tính theo a thể tích V của khối chóp S.ABCD.
A. V = 19 a 3 6
B. V = 15 a 3 6
C. V = 19 a 3 2
D. V = 15 a 3 6
Đáp án B
Phương pháp:
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
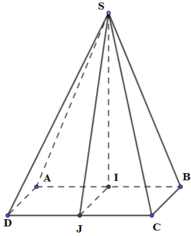
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
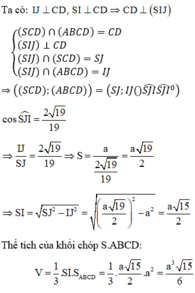
Hình chóp S.ABCD có đáy ABCDa là hình vuông cạnh a, SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy (ABCD). Biết côsin của góc tạo bởi mặt phẳng (SCD) và (ABCD) bằng 2 17 17 . Thể tích Vcủa khối chóp S.ABCD là:
A. V = a 3 13 6
B. V = a 3 17 6
C. V = a 3 17 2
D. V = a 3 13 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA=a và SA vuông góc với đáy. Tang của góc giữa đường thẳng SO và mặt phẳng (SAB) bằng
A. 2
B. 2 2
C. 5
D. 5 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA = a và SA vuông góc với đáy. Tang của góc giữa đường thẳng SO và mặt phẳng (SAB) bằng
A. 2
B. 2 2
C. 5
D. 5 5
Đáp án D
Phương pháp:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
Gọi H là trung điểm của AB => OH//AD
ABCD là hình vuông => AD ⊥ AB; OH ⊥ AB
Mà OH ⊥ SA, (vì SA ⊥ (ABCD))
=> OH ⊥ (SAB)
=>SH là hình chiếu vuông góc của SO trên mặt phẳng (SAB)
=> (SO,(SAB)) = (SO,SH) = HSO
Ta có: OH là đường trung bình của tam giác ABD 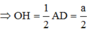
Tam giác SAH vuông tại A ![]()
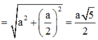
Tam giác SHO vuông tại H: 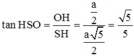

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a , SA vuông góc ABCD , SA =a√2
a) CM : BD vuông góc SAC
b) tính góc giữa SC và mp ABCD
25.
\(\lim\dfrac{3.5^n+7.7^n+9}{6.5^n+9.7^n-3}=\lim\dfrac{7^n\left[3\left(\dfrac{5}{7}\right)^n+7+9.\left(\dfrac{1}{7}\right)^n\right]}{7^n\left[6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n\right]}\)
\(=\lim\dfrac{3\left(\dfrac{5}{7}\right)^n+7+9\left(\dfrac{1}{7}\right)^n}{6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n}=\dfrac{3.0+7+9.0}{6.0+9-3.0}=\dfrac{7}{9}\)
26.
\(\lim\left(n-\sqrt{n^2-4n}\right)=\lim\dfrac{\left(n-\sqrt{n^2-4n}\right)\left(n+\sqrt{n^2-4n}\right)}{n+\sqrt{n^2-4n}}\)
\(=\lim\dfrac{4n}{n+\sqrt{n^2-4n}}=\lim\dfrac{4n}{n\left(1+\sqrt{1-\dfrac{4}{n}}\right)}\)
\(=\lim\dfrac{4}{1+\sqrt{1-\dfrac{4}{n}}}=\dfrac{4}{1+\sqrt{1-0}}=2\)
26.
\(u_1=5\)
\(u_n=405=u_1.q^{n-1}\Rightarrow q^{n-1}=\dfrac{405}{5}=81\)
\(\Rightarrow q^n=81q\)
Do \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\Rightarrow605=\dfrac{5\left(1-81q\right)}{1-q}\)
\(\Rightarrow605-605q=5-405q\)
\(\Rightarrow q=3\)
27.
a.
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow BD\perp\left(SAC\right)\)
b.
Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
Câu 5: Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O cạnh bằng a, góc giữa cạnh bên và mặt đáy 1 góc 60°. Gọi IE lần lượt là là trung điểm của cạnh BC,CD a)Chứng minh: AC vuông góc (SBD) ; BD vuông góc SA b)Chứng minh: (SBC) vuông góc (SOI) c)Tính góc giữa mặt bên và mặt đáy. d)góc giữa OE và mặt (SCD) e)Tính khoảng cách giữa SI và AB.
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc A bằng 60 o , O là tâm hình thoi, SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng 45 o . Tính theo a thể tích khối chóp SABCD.
A. 3 2 a 3 x
B. a 3 4
C. 3 a 3 8
D. 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung điểm của SC, SD (tham khảo hình vẽ bên). Tính côsin của góc giữa hai mặt phẳng G M N v à A B C D .
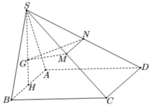
A. 2 39 39
B. 13 13
C. 3 6
D. 2 39 13