Cho hình lập phương ABCD.A'B'C'D' có tất cả các cạnh bằng 1. Gọi M là trung điểm của BB' .Tính thể tích khối A'MCD
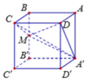
A. 1 12 .
B. 2 15 .
C. 4 15 .
D. 1 28 .
Cho hình lập phương ABCD.A'B'C'D' có tất cả các cạnh bằng 1. Gọi M là trung điểm của BB'. Tính thể tích khối A'MCD.
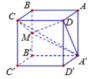
A. 1 12
B. 2 15
C. 4 15
D. 1 28
Chọn A.
Cách 1: Dùng HHKG thuần túy:
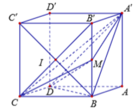
Ta có: ![]()
![]()
Gọi I là tâm của hình vuông BCC'B', suy ra: BI ⊥ B'C'
Mà ![]()
Suy ra BI ⊥ BCC'B' => BI là chiều cao của hình chóp B.A'B'CD.
Thể tích khối chóp B.A'B'CD là: ![]()
![]()
Vậy ![]()
Cách 2: Dùng hệ tọa độ Oxyz.
Chọn hệ trục tọa độ như hình vẽ.
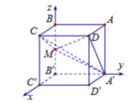
Khi đó ![]()
Suy ra
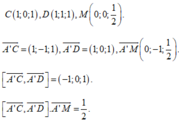
Ta có ![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN
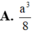
![]()
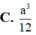
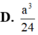
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Gọi M là trung điểm A'B' là trung điểm. Tính thể tích của khối tứ diện ADMN
A. V = a 3 3
B. V = a 3 12
C. V = a 3 6
D. V = a 3 2
Đáp án C
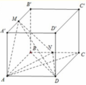
Ta có: S N A D = 1 2 d N ; A D . A D = 1 2 a 2
d M ; A B C D = A A ' = a
Do đó V M . A D N = 1 3 . A A ' . S N A D = a 3 6 .
Cho hình lập phương ABCD.A'B'C'D' cạnh 2a, gọi M là trung điểm của BB' và P thuộc cạnh sao cho D P = 1 4 D D ' . Mặt phẳng (AMP) cắt CC' tại N. Thể tích khối đa diện AMNPBCD bằng

![]()
![]()

Cho hình lập phương ABCD.A'B'C'D' cạnh 2a, gọi M là trung điểm của BB' và P thuộc cạnh DD' sao cho D P = 1 4 D D ' . Mặt phẳng (AMP) cắt CC' tại N. Thể tích khối đa diện AMNPBCD bằng
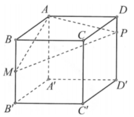
A. V = 2 a 3
B. V = 3 a 3
C. V = 9 a 3 4
D. V = 11 a 3 3
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh 2a, gọi M là trung điểm của B B ' và P thuộc cạnh D D ' sao cho D P = 1 4 D D ' . Mặt phẳng A M P cắt C C ' tại N. Thể tích khối đa diện A M N P B C D bằng
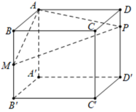
A. V = 2 a 3
B. V = 3 a 3
C. V = 9 a 3 4
D. V = 11 a 3 3
Đáp án B
Áp dụng công thức tính nhanh, ta có V A M P B C D V A B C D . A ' B ' C ' D ' = 1 2 B M B B ' + D P D D ' = 3 8 ⇒ V A M P B C D = 3 a 3 .
Cho hình lập phương ABCD.A'B'C'D' có độ dài cạnh bằng 1. Gọi M, N, P, Q lần lượt là trung điểm của A B , B C , C ' D ' và DD'. Tính thể tích khối tứ diện MNPQ
A. 3/8
B. 1/8
C. 1/12
D. 1/24
Đáp án C
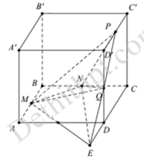
Dựng hình như hình vẽ
Ta có: V M N P Q = 1 2 V P . M N E = 1 2 . 1 3 .1. S M N E
Do M N / / A C ; M E / / B D ⇒ M N ⊥ M E ; M N = 2 2 ; M E = 2
Do đó S M N E = 1 2 ⇒ V M N P Q = 1 12
(ngoài ra các em có thể gắn các hệ trục tọa độ)
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi Mvà N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN.
A. a 3 8
B. a 3
C. a 3 12
D. a 3 24
Đáp án D
S O ' O N = 1 2 OO'.ON= 1 2 . a . a 2 = a 2 4 ; M O ' = a 2 . V M O ' O N = 1 3 M O ' . S O ' O N = a 3 24 .
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M , N, P lần lượt là trung điểm các cạnh CD, A'B', A'D' . Thể tích khối tứ diện A' MNP bằng:
A. a 3 16
B. a 3 32
C. a 3 12
D. a 3 24
Phương pháp:
Sử dụng công thức 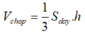
Cách giải:
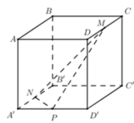
Ta có
![]()
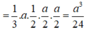
Chọn D.