Cho hàm số y = m x + 2016 m + 2017 − x − m với m là tham số thực. Gọi S là tập hợp các giá trị nguyên của m để hàm số đồng biến trên từng khoảng xác định. Tính số phần tử của S.
A.2017
B.2018
C.2016
D.2019
Cho các số a,b,c,d khác 0. Tính \(T=x^{2017}+y^{2017}+z^{2017}+t^{2017}\)
Biết x,y,z,t thỏa mãn: \(\dfrac{x^{2016}+y^{2016}+z^{2016}+t^{2016}}{a^2+b^2+c^2+d^2}=\dfrac{x^{2016}}{a^2}+\dfrac{y^{2016}}{b^2}+\dfrac{z^{2016}}{c^2}+\dfrac{t^{2016}}{d^2}\)
cho 3 số x, y, z thoả mãn x/2015=y/2016=z/2017 C/m (x-z)^3 = 8(x-y) ^2. (y-z)
Đặt x/2015=y/2016=z/2017=k
=> x=2015k
=> y=2016k
=> z=2017k
Ta có
•(x-z)3=(2015k-2017k)3=(-2k)3=-8k3 (1)
•8(x-y)2(y-z)=8(2015k-2016k)2(2016k-2017k)= 8(-k)2(-k)=-8k3 (2)
Từ (1) và (2) => (x-z)3=8(x-y)2(y-z)
Cho x,y>0 thỏa mãn
x^2015+y^2015=x^2016+y^2016=x^2017+y^2017
C/m: 1/x^2018+1/y^2018=1/x^2019+1/y^2019
tìm các số nguyên dương x,y thỏa mãn x2 +x + /-2016.y/ = (-2016)2 +2017
Ta có : \(x^2+x+\left|-2016y\right|=\left(-2016\right)^2+2017\)
=> \(x\left(x+1\right)+\left|-2016y\right|=\left(-2016\right)^2+2017\)
Ta thấy :\(\left\{{}\begin{matrix}x\left(x+1\right)⋮2\\\left|-2016y\right|⋮2\end{matrix}\right.\) \(\Rightarrow\)Vế trái là số chẵn
Mặt khác , \(\left\{{}\begin{matrix}\left(-2016\right)^2⋮2\\2017⋮̸2\end{matrix}\right.\) \(\Rightarrow\)Vế phải là số lẻ
\(\Rightarrow\)Không có x,y thuộc Z nào thỏa mãn
Cho hàm số \(y=x^2-4x+3\) . Nếu tiếp tuyến của đồ thị hàm số tại điểm M song song với đường thẳng \(-8x+y-2017=0\) thì hoành độ \(x_o\) của M là ?
Ủa hỏi mỗi hoành độ thôi hở :D?
\(f'\left(x\right)=2x-4\)
Vi \(pttt//d:y=8x+2017\Rightarrow f'\left(x\right)=8\)
\(\Rightarrow2x-4=8\Leftrightarrow x=6\)
Cho hàm số y = 1 3 x 3 - m x 2 + ( 4 m - 3 ) x + 2017 . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên .
A. m = 2
B. m = 3
C. m = 4
D. m = 1
Chọn B
Phương pháp:
Tính y', để hàm số đồng biến trên
ℝ
thì ![]() (y' = 0 tại hữu hạn điểm)
(y' = 0 tại hữu hạn điểm)
Sử dụng ![]()
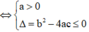
Cách giải:
Tập xác định D = ℝ
Đạo hàm ![]()
Để hàm số đồng biến trên
ℝ
thì ![]() (y' = 0 tại hữu hạn điểm)
(y' = 0 tại hữu hạn điểm)
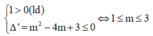
Suy ra giá trị lớn nhất của tham số m thỏa mãn ycbt là m = 3
Cho ba số x, y, z không âm thỏa mãn x + xy +y = 1; y + yz + z = 3 ; z + zx + x = 7. Tính P = x^2015 + y^2016 + z^2017
Cho ba số x, y, z không âm thỏa mãn x + xy +y = 1; y + yz + z = 3 ; z + zx + x = 7. Tính P = x^2015 + y^2016 + z^2017
Cho hàm số y = 1 3 x 3 - m x 2 + ( 4 m - 3 ) x + 2017 . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên R
A.m=2
B.m=3
C.m=4
D.m=1
Cho ba số x, y, z không âm thỏa mãn x + xy +y = 1; y + yz + z = 3 ; z + zx + x = 7.
Tính P = x^2015 + y^2016 + z^2017
\(\left\{{}\begin{matrix}x+xy+y=1\\y+yz+z=3\\z+zx+x=7\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\left(y+1\right)+\left(y+1\right)=2\\y\left(z+1\right)+\left(z+1\right)=4\\z\left(x+1\right)+\left(x+1\right)=8\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x+1\right)\left(y+1\right)=2\\\left(y+1\right)\left(z+1\right)=4\\\left(z+1\right)\left(x+1\right)=8\end{matrix}\right.\)
\(\Rightarrow\left[\left(x+1\right)\left(y+1\right)\left(z+1\right)\right]^2=64\)
\(\Rightarrow\left(x+1\right)\left(y+1\right)\left(z+1\right)=8\) ( do x,y,z không âm )
\(\Rightarrow\left\{{}\begin{matrix}x+1=2\\y+1=1\\z+1=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=0\\z=3\end{matrix}\right.\)
\(\Rightarrow P=3^{2017}+1\)