Cho parabol (P) có phương trình y = 2 x 2 − 3 x − 1 . Tịnh tiến parabol (P) theo vectơ v → − 1 ; 4 thu được đồ thị của hàm số nào dưới đây?
A. y = 2 x 2 + x + 2
B. y = 2 x 2 − 19 x + 44
C. y = 2 x 2 − 7 x
D. y = 2 x 2 + 13 x + 18
Những câu hỏi liên quan
Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto
v
→
(
-
2
;
-
1
)
biến parabol (P): y
x
2
thành parabol (P’) có phương trình: A.
y
x
2
+
4
x
-
5
B.
y
...
Đọc tiếp
Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto v → ( - 2 ; - 1 ) biến parabol (P): y = x 2 thành parabol (P’) có phương trình:
A. y = x 2 + 4 x - 5
B. y = x 2 + 4 x + 4
C. y = x 2 + 4 x + 3
D. y = x 2 - 4 x + 5
Lấy M(x; y) thuộc (P); gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto v → ( - 2 ; - 1 ) thì:
Đáp án C
Đúng 0
Bình luận (0)
Trg mp vs hệ trục tọa độ Oxy, cho phép tịnh tiến theo v = (-2 ; -1), phép tịnh tiến theo v biến parabol (P): y = x bình thành parabol (P'). Khi đó pt của (P') là?
Trong mặt phẳng tọa độ Oxy cho vectơ
v
→
-
1
;
2
,
A
3
;
5
,
B
-
1
;
1
và đường thẳng d có phương trình
x
–
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
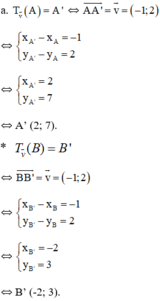
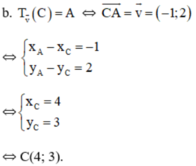
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C):
(
x
+
1
)
2
+
(
y
-
3
)
2
4
. Phép tịnh tiến theo vectơ
v
→
3
;
2
biến đường tròn (C) thành đường tròn có phương trình nào dưới đây A.
(...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): ( x + 1 ) 2 + ( y - 3 ) 2 = 4 . Phép tịnh tiến theo vectơ v → = 3 ; 2 biến đường tròn (C) thành đường tròn có phương trình nào dưới đây
A. ( x + 2 ) 2 + ( y + 5 ) 2 = 4
B. ( x - 1 ) 2 + ( y + 3 ) 2 = 4
C. ( x + 4 ) 2 + ( y - 1 ) 2 = 4
D. ( x - 2 ) 2 + ( y - 5 ) 2 = 4
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn (C)
x
+
1
2
+
(
y
-
3
)
2
4
qua phép tịnh tiến theo ve...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn (C) x + 1 2 + ( y - 3 ) 2 = 4 qua phép tịnh tiến theo vectơ v → =(3;2) là đường tròn có phương trình:
A. x + 2 2 + ( y + 5 ) 2 = 4
B. x - 2 2 + ( y - 5 ) 2 = 4
C. x - 1 2 + ( y + 3 ) 2 = 4
D. x + 4 2 + ( y - 1 ) 2 = 4
21 tháng 2 2022 lúc 21:35
Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ
biến đường thẳng Δ: x - y -1 = 0 thành đường thẳng Δ' có phương trình là
A.x - y - 1 = 0 .
B. x + y - 1 = 0 .
C. x - y - 2 = 0 .
D. x + y + 2 = 0 .
Cho vecto v (-2;1); d: 2x-3y+30 ; d1: 2x-3y-501) Viết phương trình d’ Tv(d)2) Tìm toạ độ vecto w có phương vuông góc với d để d1 Tw(d)Cho (d): 3x-y-90. Tìm phép tịnh tiến theo phương song song với trục Ox biến d thành d’ đi qua gốc toạ độ. Hãy viết phương trình d’.Trong hệ trục toạ độ Oxy, cho parabol (P): y ax^2Gọi T là phép tịnh tiến theo vecto u(m;n) và (P’) là ảnh của (P) qua phép tịnh tiến đó. Hãy viết phương trình của (P’).Cho đường thẳng Delta: 6x+2y-10. Tìm vecto u nevecto 0 để DeltaTu(D...
Đọc tiếp
Cho vecto v= (-2;1); d: 2x-3y+3=0 ; d1: 2x-3y-5=0
1) Viết phương trình d’= Tv(d)
2) Tìm toạ độ vecto w có phương vuông góc với d để d1= Tw(d)
Cho (d): 3x-y-9=0. Tìm phép tịnh tiến theo phương song song với trục Ox biến d thành d’ đi qua gốc toạ độ. Hãy viết phương trình d’.
Trong hệ trục toạ độ Oxy, cho parabol (P): y= \(ax^2\)Gọi T là phép tịnh tiến theo vecto u=(m;n) và (P’) là ảnh của (P) qua phép tịnh tiến đó. Hãy viết phương trình của (P’).
Cho đường thẳng \(\Delta\): 6x+2y-1=0. Tìm vecto u \(\ne\)vecto 0 để \(\Delta=\)Tu(\(\Delta\))
18 tháng 8 2020 lúc 17:59
Trong mặt phẳng Oxy, cho parabol đường tròn \(\left(P\right):y=x^2+6x-1\). Qua phép tịnh tiến vecto \(\overrightarrow{v}=\left(-3;-1\right)\) biến (P) thành parabol (P'). Tìm tọa độ của đỉnh (P')
Tọa độ đỉnh của \(\left(P\right)\) là \(A\left(-3;-10\right)\)
Gọi A' là đỉnh của (P') thì A' là ảnh của A qua phép tịnh tiến \(\overrightarrow{v}\)
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=-3-3=-6\\y_{A'}=-1-10=-11\end{matrix}\right.\) \(\Rightarrow A'\left(-6;-11\right)\)
Đúng 0
Bình luận (0)
1 vẽ đồ thị hàm số y= x²/2 (P) 2 bằng phép tính hãy xác định toạ độ các giáo điểm parabol (P) với đưownhf thẳng (d) có phương trình y=-1/2 x+1 3 với các giá trị nào của m thì đường thẳng (d) y=X+m a cắt parabol (P) b tiếp xúc với parabol c không cắt parabol