Cho hàm số y=f(x) xác định, liên lục trên a và có bảng biến thiên:

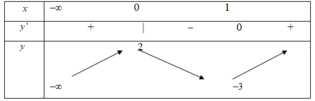
Khẳng định nào sau đây là khẳng định đúng

A. Hàm số có giá trị lớn nhất bằng 2 và có giá trị nhỏ nhất bằng -3

B. Hàm số có đúng một cực trị

C. Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1

D. Hàm số có giá trị cực tiểu bằng 2.

Cho hàm số y = f(x) có bảng biến thiên trên khoảng như sau:

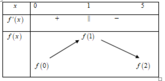
Khẳng định nào sau đây là khẳng định đúng?

A. Trên (0;2) , hàm số không có cực trị.

B. Hàm số đạt cực đại tại x=1

C. Hàm số đạt cực tiểu tại x=1

D. Giá trị nhỏ nhất của hàm số là f(0)

Cho hàm số y=f(x) xác định và liên tục trên tập D = ℝ   \   { - 1 }  và có bảng biến thiên:

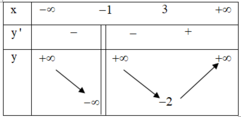
Dựa vào bảng biến thiên của hàm số y=f(x) Khẳng định nào sau đây là khẳng
định sai?

A. Giá trị nhỏ nhất của hàm số trên đoạn  [ 1 ; 8 ] bằng -2

B. Phương trình f(x)=m có 3 nghiệm thực phân biệt khi x > -2

C. Hàm số đạt cực tiểu tại x=3

D. Hàm số nghịch biến trên khoảng  ( - ∞ ; 3 )

Cho hàm số hàm số y=f(x) liên tục trên R và có bảng biến thiên:

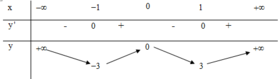
Khẳng định nào sau đây là đúng?

A. Hàm số có đúng hai điểm cực trị.

B. Hàm số có giá trị cực tiểu bằng -1 và 1

C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -3

D. Hàm số đạt cực đại tại x=0

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:

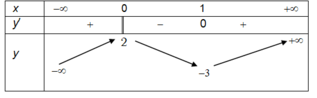
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng một cực trị

B. Hàm số có giá trị cực tiểu bằng 2

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên

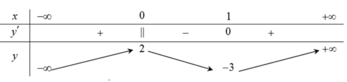
Khẳng định nào sau đây là khẳng định đúng

A. Hàm số có đúng một cực trị

B. Hàm số có giá trị cực tiểu bằng 2

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên

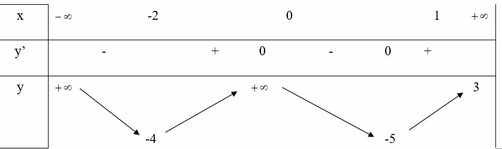
Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số cắt trục Ox tại 1 điểm

B. Đồ thị hàm số cắt trục Ox tại 2 điểm

C. Đồ thị hàm số cắt trục Ox tại 3 điểm

D. Đồ thị hàm số cắt trục Ox tại 4 điểm

Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:

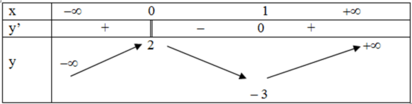
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng một cực trị

B. Hàm số có giá trị cực tiểu bằng 2

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1

Cho hàm số y = f (x) xác định, liên tục trên ℝ  và có bảng biến thiên

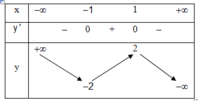
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có giá trị cực tiểu bằng -2 và giá trị cực đại bằng 2

B. Hàm số có đúng một cực trị

C. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -2

D. Hàm số đạt cực đại tại x = -1 và đạt cực tiểu tại x = 2   

Cho hàm số y = f(x) xác định, liên tục trên ℝ  và có bảng biến thiên

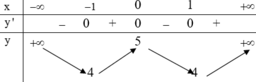
Khẳng định nào sau đây là khẳng định đúng

A. Hàm số đồng biến trong các khoảng  − ∞ ; − 1   và   0 ; 1

B. Hàm số nghịch biến trên khoảng  1 ; + ∞

C. Hàm số đồng biến trong các khoảng  − 1 ; 0   và   1 ; + ∞

D. Hàm số nghịch biến trong khoảng ( 0;1)