Cho hàm số y=f(x) thỏa mãn ∫ 0 1 f ( x ) d x = 2 và ∫ 1 5 f ( x ) d x = - 8 . Tính tích phân I = ∫ - 1 2 f 2 x - 3 d x
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) thỏa mãn f ( 0 ) = 0 ; f ' ( x ) = x x 2 + 1 . Họ nguyên hàm của hàm số g ( x ) = 4 xf ( x ) là:
A . ( x 2 + 1 ) ln ( x 2 ) - x 2 + c
B . x 2 ln ( x 2 + 1 ) - x 2
C . ( x 2 + 1 ) ln ( x 2 + 1 ) - x 2 + c
D . ( x 2 + 1 ) ln ( x 2 + 1 ) - x 2
Xét các khẳng định sau:
(1) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 1 điểm chung.
(2) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 và f(0).f(1)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 2 điểm chung.
Phát biểu nào sau đây đúng?
A. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() sai.
sai.
B. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() đúng.
đúng.
C. Khẳng định ![]() sai và khẳng định
sai và khẳng định ![]() sai.
sai.
D. Khẳng định ![]() đúng và khẳng định
đúng và khẳng định ![]() đúng.
đúng.
Đáp án C
Cả hai khẳng định đều sai vì thiếu điều kiện hàm số ![]() liên tục.
liên tục.
Xét các khẳng định sau
i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn f ( x ) ≥ f ( α ) ∀ x ∈ - 1 ; 1 .
ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β ) ∀ x ∈ - 1 ; 1 .
iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn f ( γ ) = 0
Số khẳng định đúng là
A. 3.
B. 2.
C. 1.
D. 0.
Cho hàm số y = f(x) có đạo hàm f'(x)>0, ∀ x ∈ 1 ; 2 thỏa mãn f(1) = 1, f(2) = 22/14 và ∫ 1 2 f ' x 3 x 4 d x = 7 375 . Tích phân ∫ 1 2 f x d x bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y=f(x) có đạo hàm liên tục trên ( 0 ; + ∞ ) thỏa mãn f ' ( x ) + f ( x ) x = 4 x 2 + 3 x và f(1)=2. Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x = 2 là x
A. y = 16x+20.
B. y = -16x+20
C. y = -16x-20
D. y = 16x-20.
Cho hàm số thỏa mãn f(0) khác 0, f(1)=3
f(x).f(y) = f(x+y) + f(x-y) với mọi x, y thuộc Z
Tính f(7)
Cho hàm số y=f(x) thỏa mãn f ' ( x ) + 2 x f ( x ) = e - x 2 , ∀ x ∈ R và f(1)=0 Tính giá trị f(2).
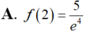
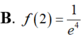
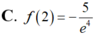
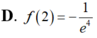
Cho hàm số y= f(x) có đạo hàm liên tục trên khoảng ![]() thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y=f(x) có đạo hàm trên R thỏa mãn f(-1)= f(3)= 0 và đồ thị hàm số y=f' (x) có dạng như hình vẽ. Hàm số y= [ f ( x ) ] 2 nghịch biến trên khoảng nào trong các khoảng sau?
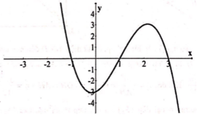
A. (-2;1).
B. (1;2).
C. (0;4).
D. (-2;2).
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
![]()
![]()
![]()
![]()