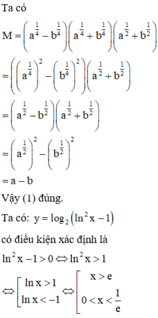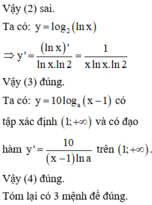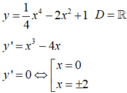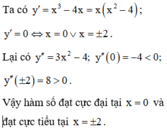Chọn phát biểu đúng khi nói về tính đơn điệu của hàm số y = a x 4 + b x 2 + c x + d , a ≠ 0 .
A. Khi a > 0 thì hàm số luôn đồng biến.
B. Khi a < 0 hàm số có thể nghịch biến trên ℝ
C. Hàm số luôn tồn tại đồng thời khoảng đồng biến và nghịch biến.
D. Hàm số có thể đơn điệu trên ℝ .




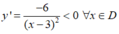

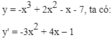
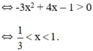
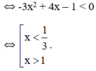
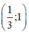
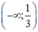 và (1; +∞)
và (1; +∞)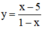
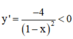 ∀ x ∈ D.
∀ x ∈ D.