Chọn D.

Ta có: TXĐ D = [1;9]

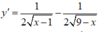
Cho y' = 0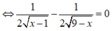 

Ta có: 

Vậy tập giá trị của hàm số là [2 2 ;4]

Đáp án là C

Đáp án C.

Hàm số có tập xác định D = [3;5]

Ta có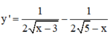 

Suy ra 

Đáp án D

Ta có g ' x = 2 x 1 ln x 2 - 1 ln x = x - 1 ln > 0 , ∀ x > 1 ⇒ g(x) đồng biến trên  1 ; + ∞

Suy ra tập giá trị của hàm số g(x) là  T = g 1 + ; g + ∞

Do 1 ln t  là hàm số nghịch biến nên g x ≥ x 2 - x 1 ln x 2 → + ∞  khi  x → + ∞

Do đó  g + ∞ = + ∞

Để tính g 1 +  đặt t = e x , ta được  g x = ∫ ln x 2 ln x e v v d v

Khi đó  g x < e 2 ln x = ∫ ln x 2 ln x d v v = x 2 ln 2

Chứng minh tương tự, ta thu được g(x) > xln(2)

Theo định lí kẹp, ta suy ra  g 1 + = ln 2

Vậy tập giá trị của hàm số đã cho là  T = ln 2 ; + ∞

Đáp án D

1. Không dịch được đề

2.

\(-1\le cos2x\le1\Rightarrow1\le y\le3\)

3.

a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)

\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)

\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)

b.

\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)

\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)

\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)

4.

\(y=\left(tanx-1\right)^2+2\ge2\)

\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

Đáp án D

Chọn D

Xét .

Tập xác định .

Ta có: .

Hàm số đạt cực tiểu tại nên .

Ta có .

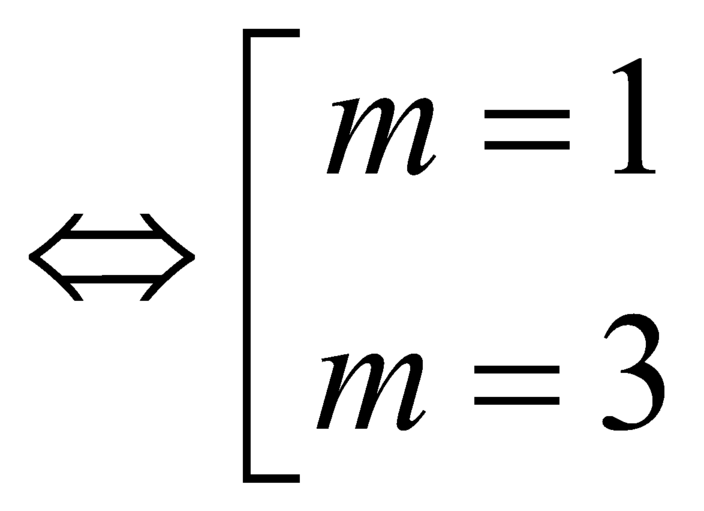Thử lại:

* Với , ta có:

.

.

.

và .

Do đó hàm số hàm số đạt cực tiểu tại .

* Với , ta có:

.

.

.

và .

Do đó hàm số hàm số không đạt cực tiểu tại x=1

Vậy với m= 1, hàm số đạt cực tiểu tại x = 1