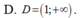Các câu hỏi tương tự
Cho hàm số
f
(
x
)
∫
1
x
d
t
t
2
+
t
(
x
1
)
Tập giá trị của hàm số là:
Đọc tiếp
Cho hàm số f ( x ) = ∫ 1 x d t t 2 + t ( x > 1 ) Tập giá trị của hàm số là:
![]()
![]()
![]()
![]()
Tìm tập giá trị T của hàm số y = x - 1 + 9 - x
A. T = [1;9]
B. T = [0;2 2 ]
C. T = (1;9)
D. T = [2 2 ;4]
Xét hàm số
f
(
t
)
9
t
9
t
+
m
2
với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) 1 với mọi số thực x, y thỏa mãn
e
x
+
y...
Đọc tiếp
Xét hàm số f ( t ) = 9 t 9 t + m 2 với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) =1 với mọi số thực x, y thỏa mãn e x + y ≤ e ( x + y ) . Tìm số phần tử của S.
A. 0
B. 1
C. Vô số
D. 2
Tìm tập xác định D của hàm số
y
l
n
(
1
-
x
)
2
Đọc tiếp
Tìm tập xác định D của hàm số y = l n ( 1 - x ) 2
![]()
![]()
![]()
![]()
Tìm giá trị lớn nhất của hàm số f(x)=x(2-ln x) trên đoạn [2;3].
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số
f
(
x
)
1
x
2
1
-
x
2
Tìm nguyên hàm của hàm số g(t) cost.f(sint) , với
t
∈
-
π
2...
Đọc tiếp
Cho hàm số f ( x ) = 1 x 2 1 - x 2 Tìm nguyên hàm của hàm số g(t) = cost.f(sint) , với t ∈ - π 2 ; π 2 là
![]()
![]()
![]()
![]()
Tìm tập hợp T tất cả các giá trị của tham số m để hàm số
y
x
3
-
2
mx
2
+
m
2
x
+
1
đạt cực tiểu tại x 1 A. B. C. D.
Đọc tiếp
Tìm tập hợp T tất cả các giá trị của tham số m để hàm số y = x 3 - 2 mx 2 + m 2 x + 1 đạt cực tiểu tại x= 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y f(x) nhận giá trị không âm và liên tục trên đoạn [0;1]. Đặt
g
(
x
)
1
+
2
∫
0
x
f
(
t
)
d
t
. Biết
g
(
x
)
≥
f
3
(
x
)
. Tích phân
∫
0
1...
Đọc tiếp
Cho hàm số y = f(x) nhận giá trị không âm và liên tục trên đoạn [0;1]. Đặt g ( x ) = 1 + 2 ∫ 0 x f ( t ) d t . Biết g ( x ) ≥ f 3 ( x ) . Tích phân ∫ 0 1 g 2 ( x ) 3 d x có giá trị lớn nhất bằng
A. 5/3.
B. 4.
C. 4/3.
D. 5.
Tìm tập xác định D của hàm số
y
ln
(
x
-
1
)
Đọc tiếp
Tìm tập xác định D của hàm số y = ln ( x - 1 )
![]()
![]()
![]()