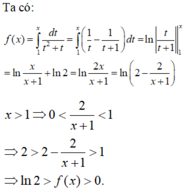Các câu hỏi tương tự
Cho hàm số
g
(
x
)
∫
x
x
2
d
t
ln
t
với x1. Tìm tập giá trị T của hàm số
Đọc tiếp
Cho hàm số g ( x ) = ∫ x x 2 d t ln t với x>1. Tìm tập giá trị T của hàm số
![]()
![]()
![]()
![]()
Cho hàm số yf(x) có đạo hàm f(x)
(
x
2
-
1
)
(
x
-
2
)
. Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số
f
(
x
2
+
m
)
có 5 điểm cực trị. Số phần tử của tập S là. A. 4 B. 1 C. 3 D. 2
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x 2 - 1 ) ( x - 2 ) . Gọi S là tập tất cả các giá trị nguyên của tham số m để hàm số f ( x 2 + m ) có 5 điểm cực trị. Số phần tử của tập S là.
A. 4
B. 1
C. 3
D. 2
Cho hàm số
f
(
x
)
có đạo hàm
f
(
x
)
(
x
2
-
9
)
(
x
2
-
3
x
)
2
,
∀
x
∈
ℝ
. Gọi T là giá trị cực đại của hàm số đã cho. Chọn khẳng định đúng
Đọc tiếp
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x 2 - 9 ) ( x 2 - 3 x ) 2 , ∀ x ∈ ℝ . Gọi T là giá trị cực đại của hàm số đã cho. Chọn khẳng định đúng
![]()
![]()
![]()
![]()
Cho F(x) là một nguyên hàm của hàm số f(x) = |1+x| - |1-x| trên tập R và thỏa mãn F(1) = 3 Tính tổng T = F(0) + F(2) + F(-3)
A. 8.
B. 12.
C. 18.
D. 10.
Gọi F(x) là một nguyên hàm của hàm số f(x)
5
x
thỏa mãn f(0)
1
ln
5
. Tính giá trị biểu thức TF(0)+F(1)+F(2)+...+F(2017)
Đọc tiếp
Gọi F(x) là một nguyên hàm của hàm số f(x)= 5 x thỏa mãn f(0)= 1 ln 5 . Tính giá trị biểu thức T=F(0)+F(1)+F(2)+...+F(2017)
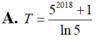
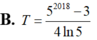
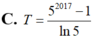
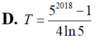
Xét hàm số
f
(
t
)
9
t
9
t
+
m
2
với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) 1 với mọi số thực x, y thỏa mãn
e
x
+
y...
Đọc tiếp
Xét hàm số f ( t ) = 9 t 9 t + m 2 với là m tham số thực. Gọi S là tập hợp tất cả các giá trị của m sao cho f(x) + f(y) =1 với mọi số thực x, y thỏa mãn e x + y ≤ e ( x + y ) . Tìm số phần tử của S.
A. 0
B. 1
C. Vô số
D. 2
Gọi F(x) là một nguyên hàm của hàm số
f
(
x
)
2
x
thỏa mãn
F
(
0
)
1
ln
2
. Tính giá trị biểu thức
T
F
(
0
)
+
F
(
1
)
...
Đọc tiếp
Gọi F(x) là một nguyên hàm của hàm số f ( x ) = 2 x thỏa mãn F ( 0 ) = 1 ln 2 . Tính giá trị biểu thức T = F ( 0 ) + F ( 1 ) + . . . + F ( 2017 )
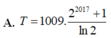
![]()
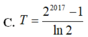
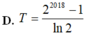
Cho hàm số
y
f
(
x
)
log
0
,
5
x
-
1
+
m
2
+
m
(m là tham số). Biết rằng có hai giá trị
m
1...
Đọc tiếp
Cho hàm số y = f ( x ) = log 0 , 5 x - 1 + m 2 + m (m là tham số). Biết rằng có hai giá trị m 1 ; m 2 để gía trị nhỏ nhất của hàm số y = f(x) trên đoạn 33 32 ; 1025 1024 bằng 13. Tính T = ( m 1 2 - m 1 ) m 2 2 - m 2
A. T = 9
B. T = 36
C. T = 4
D. T = 64
Cho hàm số y f(x) xác định trên tập số thực và có đạo hàm f(x). Đồ thị hàm số y f(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) f(4). - f(3). Giá trị nhỏ nhất của hàm số y f(x) trên đoạn [0;4] là A. f(1) B. f(0) C. f(2) D. f(4)
Đọc tiếp
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
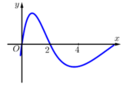
A. f(1)
B. f(0)
C. f(2)
D. f(4)