Cho hàm số y=f(x)= x 4 - 2 x 2 + 2019 . Khẳng định nào dưới đây đúng
A. f(-2)<f(3)<f(1).
B. f(-2)<f(1)<f(3).
C. f(3)<f(1)<f(-2).
D. f(1)<f(-2)<f(3)
Những câu hỏi liên quan
Cho hàm số
y
f
(
x
)
liên tục trên R và có đạo hàm
f
(
x
)
-
(
x
-
10
)
(
x
-
11
)
2
(
x
-
12
)
2019...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đạo hàm f ' ( x ) = - ( x - 10 ) ( x - 11 ) 2 ( x - 12 ) 2019 . Khẳng định nào dưới đây đúng ?
A. Hàm số đồng biến trên các khoảng (10;11) và ( 12 ; + ∞ ) .
B. Hàm số có ba điểm cực trị
C. Hàm số đồng biến trên khoảng (10;12)
D. Hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 1 và x = 3
Cho hàm số yf(x) liên tục trên R và có đạo hàm
f
’
(
x
)
(
x
+
2
)
(
x
-
1
)
2018
(
x
-
2
)
2019
. Khẳng định nào sau đây là đúng? A. Hàm số có ba điểm cực trị B. Hàm số nghịch biến trên khoảng (-2;2) C. Hàm số đạt cực đại tại điểm
x...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đạo hàm f ’ ( x ) = ( x + 2 ) ( x - 1 ) 2018 ( x - 2 ) 2019 . Khẳng định nào sau đây là đúng?
A. Hàm số có ba điểm cực trị
B. Hàm số nghịch biến trên khoảng (-2;2)
C. Hàm số đạt cực đại tại điểm x = 1 và đạt cực tiểu tại các điểm x = ± 2
D. Hàm số đồng biến trên mỗi khoảng (1;2) và (2;+∞)
Cho hàm số y f(x) xác định trên khoảng (-2;-1) và có
lim
x
→
2
-
f
(
x
)
2
,
lim
x
→
1
-
f
(
x
)
-
∞
. Hỏi khẳng định nào dưới đây là khẳng định đúng? A. Đồ thị hàm số f(x) có đúng một tiệm cận ngang là đường...
Đọc tiếp
Cho hàm số y = f(x) xác định trên khoảng (-2;-1) và có lim x → 2 - f ( x ) = 2 , lim x → 1 - f ( x ) = - ∞ . Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. Đồ thị hàm số f(x) có đúng một tiệm cận ngang là đường thẳng y = 2
B. Đồ thị hàm số f(x) có đúng hai tiệm cận ngang là các đường thẳng y = 2 và y = -1
C. Đồ thị hàm số f(x) có đúng một tiệm cận đứng là đường thẳng x = -1
D. Đồ thị hàm số f(x) có đúng hai tiệm cận đứng là các đường thẳng x = -2 và x = -1
Đáp án C
lim x → 2 - f ( x ) = 2 , lim x → 1 - f ( x ) = - ∞ nên đồ thị hàm số có duy nhất 1 đường tiệm cận đứng là x = -1
Đúng 0
Bình luận (0)
Câu4 :Cho hàm số y f(x) 2x. Khẳng định nào sau đây đúng?
A. f(0) 0
B. f(1) 6
C. f(-1) 10
D. f(2) -4
Câu 5:Một hàm số được cho bẳng công thức y f(x) x2 ( x bình phương) Khẳng định nào sau đây đúng?
A. f(1) 6
Câu6:Cho hàm số y f(x) 2 + 8x. Khẳng định nào sau đây đúng?
A. f(0) 0
B. f(1) 10
C. f(-1) 10
D. f(2) -4
Câu7:Một hàm số được cho bẳng công thức y f(x) 2x. Tính f(-5) + f(5). KẾT QUẢ ĐÚNG LÀ
A. 0
B. 25
C. 50
D. 10
Đọc tiếp
Câu4 :Cho hàm số y = f(x) = 2x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 6 C. f(-1) = 10 D. f(2) = -4 Câu 5:Một hàm số được cho bẳng công thức y = f(x) = x2 ( x bình phương) Khẳng định nào sau đây đúng? A. f(1) = 6 Câu6:Cho hàm số y = f(x) = 2 + 8x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 10 C. f(-1) = 10 D. f(2) = -4 Câu7:Một hàm số được cho bẳng công thức y = f(x) = 2x. Tính f(-5) + f(5). KẾT QUẢ ĐÚNG LÀ A. 0 B. 25 C. 50 D. 10
Cho hàm số y f(x) có đồ thị (C) xác định trên khoảng (-2;-1) và có
lim
x
→
(
−
2
)
+
f
(
x
)
2...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị (C) xác định trên khoảng (-2;-1) và có lim x → ( − 2 ) + f ( x ) = 2 , lim x → ( − 1 ) − f ( x ) = − ∞ . Khẳng định nào dưới đây đúng?
A. Đồ thị (C) có đúng hai tiệm cận ngang là đường thẳng y = 2 và y = –1
B. Đồ thị (C) có đúng một tiệm cận đứng là đường thẳng x = –1
C. Đồ thị (C) có đúng một tiệm cận ngang là đường thẳng y = 2
D. Đồ thị (C) có đúng hai tiệm cận đứng là đường thẳng x = –2 và x = –1
Cho hàm số y f(x) có
1
≤
f
(
x
)
≤
4
với mọi
x
∈
2
;
5
. Hỏi khẳng định nào dưới đây là khẳng định đúng? A.
3
≤
f
(
5
)
-
f
(
2
)
≤
12
B.
-
12
≤...
Đọc tiếp
Cho hàm số y = f(x) có 1 ≤ f ' ( x ) ≤ 4 với mọi x ∈ 2 ; 5 . Hỏi khẳng định nào dưới đây là khẳng định đúng?
A. 3 ≤ f ( 5 ) - f ( 2 ) ≤ 12
B. - 12 ≤ f ( 5 ) - f ( 2 ) ≤ 3
C. 1 ≤ f ( 5 ) - f ( 2 ) ≤ 4
D. - 4 ≤ f ( 5 ) - f ( 2 ) ≤ - 1
Chọn A.
Đầu tiên ta phải nhận dạng được f(5) - f(2) = ∫ 2 5 f ' ( x ) d x
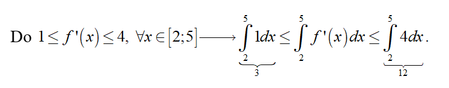
Vậy 3 ≤ f ( 5 ) - f ( 2 ) ≤ 12
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định và có đạo hàm yf(x). Đồ thị của hàm số y f(x) như hình dưới đây.Khẳng định nào sau đây là đúng? A. Hàm số
y
f
x
có ba điểm cực trị. B. Hàm số
y
f
x
đồng biến trên khoảng
−
∞
;
2
C. Hàm số
y
f...
Đọc tiếp
Cho hàm số y = f(x) xác định và có đạo hàm y=f'(x). Đồ thị của hàm số y = f'(x) như hình dưới đây.
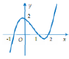
Khẳng định nào sau đây là đúng?
A. Hàm số y = f x có ba điểm cực trị.
B. Hàm số y = f x đồng biến trên khoảng − ∞ ; 2
C. Hàm số y = f x nghịch biến trên khoảng 0 ; 1
D. Hàm số y = f x đồng biến trên khoảng − ∞ ; − 1
Đáp án A
Phương pháp: Quan sát đồ thị hàm số y = f ' x để tìm khoảng dương, âm của f ' x , từ đó tìm được khoảng đồng biến, nghịch biến của f x .
Cách giải:
Từ đồ thị hàm số y = f ' x suy ra hàm số y = f x nghịch biến trên − ∞ − 1 và 1 ; 2 (làm y'âm) và đồng biến trên − 1 ; 1 (làm y'dương).
Suy ra B, C, D sai và A đúng.
Chú ý khi giải:
HS có thể nhầm lẫn thành đồ thị hàm số y = f x do đọc không kĩ đề dẫn đến chọn sai đáp án.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có
lim
x
→
0
+
f
(
x
)
-
∞
và
lim
x
→
2
+
f
(
x
)
-
∞
Khẳng định nào sau đây là khẳng định đúng? A. Đồ thị...
Đọc tiếp
Cho hàm số y = f(x) có lim x → 0 + f ( x ) = - ∞ và lim x → 2 + f ( x ) = - ∞
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số đã cho không có tiệm cận đứng.
B. Đồ thị hàm số đã cho có đúng một tiệm cận đứng.
C. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng y = 0 và y = 2.
D. Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 0 và x = 2.
Đáp án D.
Đồ thị hàm số đã cho có hai tiệm cận đứng là các đường thẳng x = 0 và x = 2
Đúng 0
Bình luận (0)
Cho hàm số y f (x) có
f
(
x
)
(
2
x
-
1
)
x
2
(
1
-
x
)
2
Khẳng định nào sau đây là khẳng định đúng? A. Hàm số đã cho có đúng một cực trị. B. Hàm số đã cho không có cực trị. C. Hàm số đã cho có hai cực trị. D. Hàm số đã cho có ba cực trị
Đọc tiếp
Cho hàm số y = f (x) có f ' ( x ) = ( 2 x - 1 ) x 2 ( 1 - x ) 2 Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đã cho có đúng một cực trị.
B. Hàm số đã cho không có cực trị.
C. Hàm số đã cho có hai cực trị.
D. Hàm số đã cho có ba cực trị
