Trong mặt phẳng tọa độ Oxy ảnh của đường tròn C : x + 1 2 + y − 3 2 = 4 qua phép tịnh tiến theo vectơ v → = 3 ; 2 là đường tròn có phương trình:
A. x + 2 2 + y + 5 2 = 4
B. x − 2 2 + y − 5 2 = 4
C. x − 1 2 + y + 3 2 = 4
D. x + 4 2 + y − 1 2 = 4
trong mặt phẳng tọa độ Oxy, hãy tìm ảnh của đường tròn (C') qua phép quay tâm O, góc quay 90 độ
(C): (x-2)^2 + (y-1)^2 = 1
Trong mặt phẳng tọa độ Oxy ảnh của đường tròn (C) x + 1 2 + ( y - 3 ) 2 = 4 qua phép tịnh tiến theo vectơ v → =(3;2) là đường tròn có phương trình:
A. x + 2 2 + ( y + 5 ) 2 = 4
B. x - 2 2 + ( y - 5 ) 2 = 4
C. x - 1 2 + ( y + 3 ) 2 = 4
D. x + 4 2 + ( y - 1 ) 2 = 4
Trong mặt phẳng tọa độ Oxy , tìm phương trình đường tròn (D') là ảnh của đường tròn (D): (x-1)² +(y+2)²=6 qua T véctơ v với véctơ v =(1;2)
Đường tròn (D) tâm \(I\left(1;-2\right)\) bán kính \(R=\sqrt{6}\)
\(\Rightarrow\) (D') là đường tròn tâm I' là ảnh của I qua phép tịnh tiện \(\overrightarrow{v}\) và bán kính \(R'=R=\sqrt{6}\)
\(\left\{{}\begin{matrix}x'=1+1=2\\y'=-2+2=0\end{matrix}\right.\) \(\Rightarrow I'\left(2;0\right)\)
Phương trình (D'):
\(\left(x-2\right)^2+y^2=6\)
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có phương trình: x − 3 2 + y + 1 2 = 9 .
Hãy viết phương trình của đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I(1; 2) tỉ số k = -2
Ta có A(3;−1) là tâm của (C) nên tâm A' của (C') là ảnh của A qua phép vị tự đã cho. Từ đó suy ra A′ = (−3;8). Vì bán kính của (C) bằng 3, nên bán kính của (C') bằng |−2|.3 = 6
Vậy (C') có phương trình: x + 3 2 + y − 8 2 = 36 .
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x 2 + y 2 + 2 x - 4 y + 1 = 0 . Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số k=-2 có phương trình là
A. x 2 + y 2 + 4 x - 8 y + 4 = 0
B. x 2 + y 2 - 4 x + 8 y + 4 = 0
C. x 2 + y 2 + 4 x - 8 y + 4 = 0
D. x 2 + y 2 + 4 x - 8 y + 2 = 0
Trong mặt phẳng tọa độ Oxy, cho đường tròn C : x 2 + y 2 + 2 x - 4 y + 1 = 0 . Ảnh của đường tròn (C) qua phép vị tự tâm O tỷ số
k = 2 có phương trình là
A. x 2 + y 2 + 4 x - 8 y + 4 = 0
B. x 2 + y 2 - 4 x + 8 y + 4 = 0
C. x 2 + y 2 + 4 x - 8 y - 4 = 0
D. x 2 + y 2 + 4 x - 8 y + 2 = 0
Trong mặt phẳng Oxy cho đường tròn (C): x − 1 2 + y − 2 2 = 9 . Viết phương trình đường tròn ảnh của đường tròn đã cho qua phép quay Q 0 ; − 90 ο với O là gốc tọa độ.
(C) có tâm I(1;2), bán kính R = 3.
Gọi I’; R lần lượt là tâm và bán kính của đường tròn ảnh, ta có:
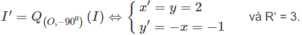
Vậy phương trình (C’) là x − 2 2 + y + 1 2 = 9 .
Trong mặt phẳng tọa độ Oxy cho điểm A(4; – 1), đường thẳng (d) : 3x – 2y + 1 = 0 và đường tròn (C) :
x^2 + y^2 - 2x + 4y -4 = 0
a. Tìm tọa độ A’ và phương trình (d’) lần lượt là ảnh của A và (d) qua phép tịnh tiến theo vectơ v = (– 2; 3)
b. Tìm phương trình đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục là đường thẳng (D) : x – y = 0
Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(3;-2), bán kính 3.
a. Viết phương trình của đường tròn đó.
b. Viết phương trình ảnh của đường tròn (I;3) qua phép tịnh tiến theo vectơ v=(-2 ;1).
c. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng trục Ox.
d. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng qua gốc tọa độ
a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
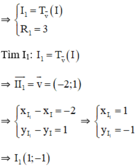
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒ 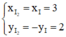 ⇒ I2(3; 2)
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒ 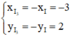
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.