Cho tam giác ABC có phương trình canh BC: 4x – y + 3 = 0 và hai đường phân giác trong của góc B, góc C lần lượt có phương trình x – 2y + 1 = 0; x + y + 3 = 0. Viết phương trình các cạnh còn lại của tam giác ABC.
mn giúp mình câu này với ạ
Cho tam giác ABC có A(2; -1) và các đường phân giác trong góc B và C lần lượt
có phương trình: x - 2y + 1= 0 ; x + y + 3 = 0.
Lập phương trình đường thẳng BC.
Gọi D là giao điểm của hai đường phân giác trong góc B và góc C
+) Trên BC lấy điểm M sao cho: AM vuông BD tại H
=> Đường thẳng AM \(\perp\)BH => AM có dạng: 2x + y + a = 0
mà A ( 2; -1) \(\in\)AM => 2.2 + ( -1) + a = 0 <=> a = -3
=> phương trình đt: AM : 2x + y - 3 = 0
H là giao của AM và BD => Tọa độ điểm H là nghiệm hệ: \(\hept{\begin{cases}x-2y+1=0\\2x+y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\)=> H ( 1; 1)
Lại có: BH vừa là đường cao vừa là đường phân giác \(\Delta\)ABM => \(\Delta\)ABM cân => H là trung điểm AM
=> \(\hept{\begin{cases}x_M=2x_H-x_A=2.1-2=0\\y_M=2y_H-y_B=2.1-\left(-1\right)=3\end{cases}}\)=> M ( 0; 3 )
+) Trên BC lấy lấy điêm N sao cho AN vuông CD tại K
Làm tương tự như trên ta có:
AN có dạng: x - y + b = 0 mà A thuộc AN => 2 + 1 + b = 0 => b = - 3
K là giao điểm của AN và CD => K ( 0; -3 )
K là trung điểm AN => N ( -2; -5 )
=> Đường thẳng BC qua điểm M và N
\(\overrightarrow{MN}\left(-2;-8\right)\)=> VTPT của BC là: \(\overrightarrow{n}\left(8;-2\right)\)
=> Phương trình BC : \(8\left(x-0\right)+\left(-2\right)\left(y-3\right)=0\)
<=> 4x -y + 3 = 0
Vậy: BC : 4x - y + 3 = 0
Cho ∆ABC có A(2;-1) và các đường phân giác trong của góc B và C lần lượt có phương trình x-2y +1=0; x+y+3 =0. Lập phương trình đường thẳng BC.
Hướng dẫn:
Qua đường phân giác trong góc B lấy điểm B' đối xứng với A => B' thuộc BC và tìm được tọa độ B'
Qua đường phân giác trong góc C lấy điểm C' đối xứng với A => C' thuộc BC và tìm được tọa độ C'
=> Phương trình BC đi qua B' và C' .
Cho tam giác ABC có A(2;−1). Đường phân giác trong góc B và C có phương trình lần
lượt là d1 :x−2y+1=0 và d2 :x+y+3=0. Viết phương trình đường thẳng chứa các cạnh của tam giác ABC.
Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}4x-y+3=0\\x-2y+1=0\end{matrix}\right.\) \(\Rightarrow B\left(-\dfrac{5}{7};\dfrac{1}{7}\right)\)
Tọa độ C là nghiệm: \(\left\{{}\begin{matrix}4x-y+3=0\\x+y+3=0\end{matrix}\right.\) \(\Rightarrow C\left(-\dfrac{6}{5};-\dfrac{9}{5}\right)\)
Phương trình đường thẳng qua C và vuông góc phân giác góc B:
\(2\left(x+\dfrac{6}{5}\right)+1\left(y+\dfrac{9}{5}\right)=0\Leftrightarrow2x+y+\dfrac{21}{5}=0\)
Gọi E là hình chiếu của C lên phân giác góc B \(\Rightarrow\left\{{}\begin{matrix}2x+y+\dfrac{21}{5}=0\\x-2y+1=0\end{matrix}\right.\) \(\Rightarrow E\left(-\dfrac{47}{25};-\dfrac{11}{25}\right)\)
Gọi F là điểm đối xứng E qua phân giác góc B \(\Rightarrow\) F thuộc AB đồng thời E là trung điểm CF \(\Rightarrow F\left(-\dfrac{64}{25};\dfrac{23}{25}\right)\)
\(\Rightarrow\overrightarrow{BF}\Rightarrow\) pt BF (chính là phương trình AB)
Làm tương tự với AC
Tam giác ABC biết A (2;-1) và phương trình hai đường phân giác trong của góc B và góc C lần lượt là d: x - 2y + 1=0, d2 : 2x - 3y + 6 = 0 . Xác định tọa độ B, C.
Cho tam giác ABC, biết A(2;-1) và 2 phân giác trong của góc B, C lần lượt là: x-2y+1 =0; x+y+3 =0. Hãy lập phương trình các cạnh.
Cho tam giác ABC có phương trình các cạnh AB. x+y-1= 0; AC: 7x- y+2=0 và BC: 10x+ y-19=0. Viết phương trình đường phân giác trong góc A của tam giác ABC.
A. 12x+ 4y-3= 0
B. 2x-6y+7= 0
C. 12x+ 6y+ 5= 0
D. 2x+6y-7=0
Đáp án B
Do AB và BC cắt nhau tại B nên toa độ điểm B là nghiệm hệ phương trình

Do đó: B( 2; -1)
Tương tự: tọa độ điểm C( 1; 9)
PT các đường phân giác góc A là:
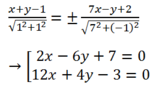
Đặt T1(x; y) = 2x- 6y+ 7 và T2= 12x+ 4y-3 ta có:
T1(B). T1(C) < 0 và T2(B) T2(C) >0.
Suy ra B và C nằm khác phía so với đường thẳng 2x-6y+7= 0 và cùng phía so với đường thẳng: 12x+ 4y- 3= 0.
Vậy phương trình đường phân giác trong góc A là: 2x- 6y+ 7= 0.
Câu 1: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có \(A(1;3)\) và hai đường trung tuyến xuất phát từ B,C lần lượt có phương trình \(y-1=0\) và \(x-2y+1=0\)
a) Viết phương trình đường tròn đường kính OA
b) Viết phương trình 3 đường thẳng chứa 3 cạnh của tam giác ABC
Câu 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có \(A(-1;-3)\), đương trung trực của cạnh AB có phương trình \(3x+2y-4=0\), trọng tâm\(G(4;-2)\)
a) Viết PTTS,TQ của đt chứa cạnh AB của tam giác ABC
b) Tìm tọa độ trung điểm M của cạnh BC tam giác ABC
c) Tìm tọa độ điểm B,C của tam giác ABC
Câu 3:Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh \(A(3;0)\) và phương trình 2 đường cao \((BB'):2x+2y-9-0\) và \((CC'):3x-12y-1=0\)
a) Viết PTTQ cuả các đt lần lượt chứa các cạnh AB,AC của tam giác ABC
bTìm tọa độ điểm B,C và viết phương trình cạnh BC của tam giác ABC
Câu 4: Trong hệ trục tọa độ Oxy, cho elip (E) có pt:\(x^2+16y^2=16\). Tìm tọa độ có đỉnh, tiêu diểm độ dài trục lớn, trục bé của elip (E)
1.
\(\overrightarrow{OA}=\left(1;3\right)\Rightarrow OA=\sqrt{10}\)
Gọi I là trung điểm OA \(\Rightarrow I\left(\dfrac{1}{2};\dfrac{3}{2}\right)\)
Phương trình đường tròn đường kính OA nhận I là trung điểm và có bán kính \(R=\dfrac{OA}{2}=\dfrac{\sqrt{10}}{2}\):
\(\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{3}{2}\right)^2=\dfrac{5}{2}\)
b.
Gọi 2 trung tuyến là BN và CM (với M, N là trung điểm AB và AC)
B thuộc BN nên tọa độ có dạng: \(\left(b;1\right)\)
M là trung điểm AB \(\Rightarrow M\left(\dfrac{b+1}{2};2\right)\)
M thuộc CM nên tọa độ thỏa mãn:
\(\dfrac{b+1}{2}-4+1=0\Rightarrow b=5\Rightarrow B\left(5;1\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(4;-2\right)\Rightarrow\) pt AB: \(\left\{{}\begin{matrix}x=1+2t\\y=3-t\end{matrix}\right.\)
Gọi G là trọng tâm tam giác ABC \(\Rightarrow\) G là giao điểm BN và CM
Tọa độ G thỏa mãn: \(\left\{{}\begin{matrix}y-1=0\\x-2y+1=0\end{matrix}\right.\) \(\Rightarrow G\left(1;1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=3x_G-x_A-x_B=-3\\y_C=3y_G-y_A-y_B=-1\end{matrix}\right.\) \(\Rightarrow C\left(-3;-1\right)\)
Biết tọa độ C, A, B bạn tự viết pt 2 cạnh còn lại
2.
AB vuông góc với trung trực của AB nên nhận (2;-3) là 1 vtpt và (3;2) là 1 vtcp
Phương trình tham số:
\(\left\{{}\begin{matrix}x=-1+3t\\y=-3+2t\end{matrix}\right.\)
Phương trình tổng quát:
\(2\left(x+1\right)-3\left(y+3\right)=0\Leftrightarrow2x-3y-7=0\)
b. Câu này tìm trung điểm của AB hay BC nhỉ? Ta chỉ có thể tìm được trung điểm BC sau khi hoàn thành câu c (nghĩa là thứ tự bài toán bị ngược)
Gọi N là trung điểm AB \(\Rightarrow\) tọa độ N thỏa mãn:
\(\left\{{}\begin{matrix}2x-3y-7=0\\3x+2y-4=0\end{matrix}\right.\) \(\Rightarrow N\left(2;-1\right)\)
N là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}x_B=2x_N-x_A=5\\y_B=2y_N-y_A=1\end{matrix}\right.\) \(\Rightarrow B\left(5;1\right)\)
G là trọng tâm tam giác nên: \(\left\{{}\begin{matrix}x_C=3x_G-x_A-x_B=8\\y_C=3y_G-y_A-y_B=-4\end{matrix}\right.\) \(\Rightarrow C\left(8;-4\right)\)
\(\Rightarrow M\left(\dfrac{13}{2};-\dfrac{3}{2}\right)\)
Câu 3 đơn giản bạn tự làm (AC vuông góc BB' nên nhận (1;-1) là 1 vtpt, AB vuông góc CC' nên nhận (4;1) là 1 vtpt).
Câu b thì B là giao điểm AB và BB', C là giao điểm AC và CC'
Câu 4.
\(x^2+16y^2=16\Leftrightarrow\dfrac{x^2}{16}+\dfrac{y^2}{1}=1\Rightarrow\left\{{}\begin{matrix}a=4\\b=1\end{matrix}\right.\) \(\Rightarrow c^2=15\Rightarrow c=\sqrt{15}\)
Các đỉnh có tọa độ lần lượt: \(\left(4;0\right);\left(-4;0\right);\left(0;1\right);\left(0;-1\right)\)
Tiêu điểm: \(F_1\left(-\sqrt{15};0\right);F_2\left(\sqrt{15};0\right)\)
Độ dài trục lớn: \(2a=8\)
Độ dài trục bé: \(2b=2\)