Một nguồn sóng o dao động theo phương trình u 0 (t) = Acos100 π t. Sóng truyền từ o đến M cách nó 30 cm với tốc độ 10 m/s. Phương trình dao động của M là

A. u M (t) = Acos(100 π t + 3 π /2)

B.  u M (t) = Acos100 π t.

C.  u M (t) = Acos(100 π t - 3 π )

D.  u M (t) = Acos(100 π t +  π )

Hai dao động điều hoà cùng phương, cùng tần số có phương trình lần lượt là : x 1  = 3cos(5 π t/2 +  π /6)(cm) và  x 2  = 3cos(5 π t/2 + 3 π /3)(cm). Biên độ và pha ban đầu của dao động tổng hợp là

A. 6 cm ;  π /4 rad.           B. 5,2 cm ; π /4 rad.

C. 5,2 cm ;  π /3 rad.        D. 5,8 cm ;  π /4 rad.

Tìm góc α ∈ {π/6;π/4;π/3;π/2} để phương trình cos2x+ 3 sin2x-2cosx= 0 tương đương với phương trình c o s ( 2 x - α ) = cos x  

A.  α = π / 6

B.  α = π / 4

C.  α = π / 2

D.  α = π / 3

Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó:

V H V ABCD . A ' B ' C ' D '

A. π /6              B.  π /4

C.  π /3              D.  π /( 3 )

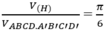
Khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm 1/4 π (H) thì dòng điện trong đoạn mạch là dòng điộn một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp xoay chiều u = 150.1/ π .cos120 π t(V) thì biểu thức của cường độ dòng điện trong đoạn mạch là :

A. i = 5 2 cos(120 π t +  π /4) (A).

B. i = 5 2 cos(120 π t -  π /4) (A).

C. i = 5cos(120 π t -  π /4) (A).

D. i = 5cos(120 π t +  π /4) (A).

Hai dao động điều hoà cùng phương, cùng tần số có phương trình lần lượt là : x 1  = 5cos( π t/2 + π /4)(cm) và  x 2  = 5cos( π t/2 + 3 π /4)(cm). Biên độ và pha ban đầu của dao động tổng hợp là

A. 5 cm ;  π /2 rad.        B. 7,1 cm ; 0 rad.

C. 7,1 cm ;  π /2 rad.        D. 7,1 cm ;  π /4 rad.

Mạch dao động điện từ gồm cuộn cảm thuần có độ tự cảm 1/ π (mH) và tu điên có điện dung 4/ π  (nF). Tần số dao động riêng của mạch là

A. 5 π 10 5  (Hz).        B. 2,5 π 10 5  (Hz).

C. 5 π 10 6  (Hz).        D. 2,5 π 10 6  (Hz).