Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh 2a và 0 S B A ^ = S C A ^ = 90 0 . Biết góc giữa đường thẳng SA và mặt đáy bằng 45 0 . Tính khoảng cách từ điểm B đến mặt phẳng (SAC).
A. 15 5 a
B. 2 15 5 a
C. 2 15 3 a
D. 2 51 5 a
Những câu hỏi liên quan
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và góc giữa cạnh bên và đáy bằng
45
o
. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp tam giác ABC là A.
πa
2
12
B.
πa
2
3
C.
πa
2...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và góc giữa cạnh bên và đáy bằng 45 o . Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp tam giác ABC là
A. πa 2 12
B. πa 2 3
C. πa 2 5 3
D. πa 2 3 5
Đáp án C
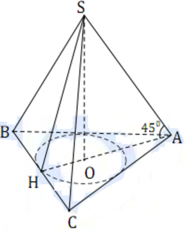
Gọi O là tâm đường tròn nội tiếp ∆ ABC.Theo giả thiết, góc giữa cạnh bên và đáy chính là góc giữa SA và OA hay S A O ^ = 45 o .Diện tích xung quanh cần tính là: S x q = π R l
Tam giác ABC đều cạnh 2a nên AH =a 3
Suy ra:
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và góc giữa cạnh bên và đáy bằng
45
°
. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp tam giác ABC là A.
πa
2
12
.
B.
πa
2
3
.
C. ...
Đọc tiếp
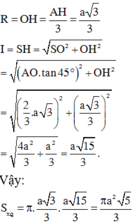
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và góc giữa cạnh bên và đáy bằng 45 ° . Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp tam giác ABC là
A. πa 2 12 .
B. πa 2 3 .
C. πa 2 5 3 .
D. πa 2 3 5 .
Đáp án C
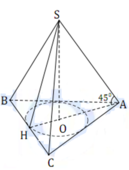
Gọi O là tâm đường tròn nội tiếp tam giác ABC.
Theo giả thiết, góc giữa cạnh bên và đáy chính là góc giữa SA và OA hay SAO ⏜ = 45 ° .
Diện tích xung quanh cần tính là: S xq = πRl
Tam giác ABC đều cạnh 2a nên AH = a 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ điểm S đến (ABC)? A.
a
3
B.
2
a
3
C.
a
6
D.
a
3...
Đọc tiếp
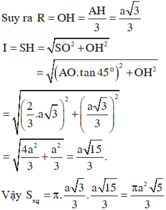
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ điểm S đến (ABC)?
A. a 3
B. 2 a 3
C. a 6
D. a 3 2
Đáp án A
Phương pháp: Hai mặt phẳng vuông góc, đường thẳng nằm trong mặt này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.
Cách giải:
Gọi H là trung điểm của AB ta có 
Tam giác SAB đều cạnh 2a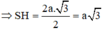 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ điểm S đến (ABC)? A.
a
3
B.
2
a
3
C.
a
6
D.
a
3
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách từ điểm S đến (ABC)?
A. a 3
B. 2 a 3
C. a 6
D. a 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tâm giác SAB đều và nằm trong mặt phẳng đáy. Tính khoảng cách từ điểm S đến mặt phẳng (ABC)
Chắc là tam giác SAB nằm trong mp vuông góc với đáy?
Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(SAB\right)\)
\(\Rightarrow SH=d\left(S;\left(ABC\right)\right)\)
\(SH=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\)
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có cạnh bên bằng 2a, góc giữa cạnh bên và mặt đáy bằng 60 độ. Tính thể tích của khối nón có đỉnh là S và đáy là đường ngoại tiếp tam giác ABC
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\)
\(\Rightarrow\widehat{SAO}=60^0\Rightarrow AO=SA.cos60^0=a\)
\(R=a;l=2a\Rightarrow h=SO=\sqrt{\left(2a\right)^2-a^2}=a\sqrt{3}\)
\(V=\dfrac{1}{3}\pi R^2h=\dfrac{\sqrt{3}}{3}\pi a^3\)
Đúng 1
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a, cạnh bên SB vuông góc với mặt phẳng
A
B
C
,
S
B
2
a
.
Tính thể tích khối chóp S,ABC. A.
a
3
4
B.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a, cạnh bên SB vuông góc với mặt phẳng A B C , S B = 2 a . Tính thể tích khối chóp S,ABC.
A. a 3 4
B. a 3 3 6
C. 3 a 3 4
D. a 3 3 2
Đáp án B
Ta có: V S . A B C = 1 3 S B . S A B C = 1 3 .2 a . a 2 3 4 = a 3 3 6
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và mặt đáy bằng
60
°
. Khoảng cách từ điểm S đến mặt đáy (ABC) là
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và mặt đáy bằng 60 ° . Khoảng cách từ điểm S đến mặt đáy (ABC) là
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , góc giữa cạnh bên và mặt đáy bằng 60 ° . Khoảng cách từ điểm S đến mặt đáy (ABC) là
A. a
B. 2 a
C. 3 a
D. 2a
Đáp án D
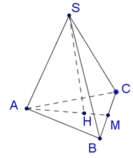
Gọi H là trọng tâm tam giác ABC, vì S.ABC là hình chóp tam giác đều nên SH vuông góc với (ABC).
Vậy . Theo bài ra ta có góc S A H ^ = 60 °
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều
S
.
ABC
có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt đáy bằng
60
o
. Khoảng cách từ điểm S đến mặt đáy
ABC
là A. 2a B.
2
a
C.
3
a
D. a
Đọc tiếp
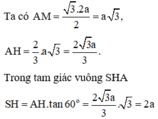
Cho hình chóp tam giác đều S . ABC có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt đáy bằng 60 o . Khoảng cách từ điểm S đến mặt đáy ABC là
A. 2a
B. 2 a
C. 3 a
D. a
