Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Tìm tất cả các giá trị thực của tham số m để hàm số y=(m-3)x-(2m+1)cosx nghịch biến trên R.
A.
B. không có m
C. 
D. 
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = | x | 3 - ( 2 m + 1 ) x 2 + 3 m | x | - 5 có 3 điểm cực trị.
A. - ∞ ; 1 4
B. 1 ; + ∞
C. ( - ∞ ; 0 ]
D. 0 ; 1 4 ∪ 1 ; + ∞
1. Tìm tất cả các giá trị thực của tham số m để hàm số y= mx - sin3x đồng biến trên khoảng ( trừ vô cùng ; cộng vô cùng) 2. Tìm tất cả các giá trị thực của tham số m để hàm số y = x + mcosx đồng biến trên khoảng( trừ vô cùng ; cộng vô cùng)
1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)
Tìm tất cả các giá trị thực của tham số m để hàm số y = 1 3 sin 3 x + m sin x + 2 m − 3 đạt cực đại tại x = π 3
A. không có giá trị m
B. m = 1
C. m = 2
D. m = − 2
Đáp án C
Ta có: y ' = cos 3 x + m . cos x và y ' ' = − 3 sin 3 x − m . sin x
Để hàm số đạt cực đại tại:
x = π 3 ⇒ y ' π 3 = 0 ⇒ − 1 + m 2 = 0 ⇔ m = 2.
Với m = 2 ⇒ y ' ' π 3 = − 3 sin π − 2 sin π 3 < 0
nên hàm số đạt cực đại tại x = π 3
Cho hàm số y = 2 x 3 - 3 m x 2 + 3 ( 5 m 2 + 1 ) x - 3 s i n x với m là tham số thực. Tìm tập hợp tất cả các giá trị của m để hàm số đồng biến trên (l;3).
A . m ≥ 1
B . m ≤ - 1
C . m > 0
D . m ∈ R
Cho hàm số f x = x - 3 2 x - 3 k h i x ≠ 3 m k h i x = 3 . Tìm tất cả các giá trị của tham số thực m để hàm số liên tục tại x = 3.
A. m ∈ ∅
B. m ∈ R
C. m = 1
D. m = - 1
- Hàm số đã cho xác định trên R.
- Ta có:
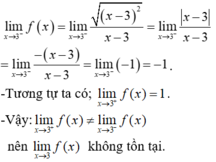
- Vậy với mọi m, hàm số đã cho không liên tục tại x = 3.
Do đó đáp án đúng là A.
Câu 8 : Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m+1\right)x-1\) đạt cực đại tại x=\(-\)2
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x - 2 x 2 - m x + 1 có đúng 3 đường tiệm cận.
A. -2<m<2
B. m > 2 m < - 2 h o ặ c m ≠ - 5 2
C. m>2 hoặc m<-2
D. m > 2 m ≠ 5 2 hoặc m<-2
