Cho mặt phẳng (P): 2x+2y-2z+15=0 và mặt cầu (S): x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 . Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu(S) là
A. 3 3 2
B. 3
C. 3 2
D. 3 3
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): \(x^2+y^2+z^2-2x+6y-8z-10=0\) và mặt phẳng (P): \(x+2y-2z=0\). Viết phương trình mặt phẳng (Q) song song với (P) và tiếp xúc với (S).
Cho mặt phẳng P : 2 x + 2 y - 2 z + 15 = 0 và mặt cầu S : x 2 + y 2 + z 2 - 2 y - 2 z - 2 = 0 . Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là:
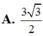
![]()
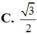
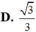
Đáp án A.
Mặt cầu (S) có tâm I(0;1;1) và bán kính R = 3
Gọi H là hình chiếu của I trên (P) và A là giao điểm của IH với (S)
Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặtcầu (S) là đoạn AH
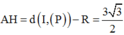
Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1;0;1) và B(-1;1;0), mặt phẳng (P):\(x+y-2z-5=0\) và mặt cầu \(\left(S\right):x^2+y^2+z^2-2x+2y-6=0\).
Viết phương trình mặt phẳng (Q), biết (Q) vuông góc với (P), song song với đường thẳng AB và tiếp xúc với mặt cầu (S)
Mặt phẳng (P) có vec tơ pháp tuyến \(\overrightarrow{n}=\left(1;1;-2\right);\overrightarrow{AB}=\left(-2;1;-1\right)\)
Ta có \(\left[\overrightarrow{n};\overrightarrow{AB}\right]=\left(1;5;3\right)\)
(Q) vuông góc với (P), song song với đường thẳng AB suy ra (Q) có vectơ pháp tuyến là \(\left[\overrightarrow{n_1};\overrightarrow{AB}\right]=\left(1;5;3\right)\) nên phương trình mặt phẳng (Q) có dạng \(x+5y+3z+m=0\)
Mặt cầu (S) có tâm \(I\left(1;-1;1\right)\), bán kính R = 3
Mặt phẳng (Q) tiếp xúc với (S) có \(d\left(I,\left(Q\right)\right)=R\Leftrightarrow\frac{\left|1-5+3+m\right|}{\sqrt{35}}\)
\(\Leftrightarrow\left|m-1\right|=3\sqrt{35}\Leftrightarrow\begin{cases}m=1+3\sqrt{35}\\m=1-3\sqrt{35}\end{cases}\)
- Với \(m=1+3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1+3\sqrt{35}=0\)
- Với \(m=1-3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1-3\sqrt{35}=0\)
Cho mặt cầu (S): x 2 + y 2 + z 2 - 2x + 4y - 2z - 3 = 0 cắt 2 mặt phẳng (P): x - 2y + z = 0 và (Q): x - z - 2 = 0 theo các đường tròn giao tuyến với bán kính r 1 ; r 2 . Khi đó tỉ số r 1 r 2 bằng
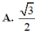
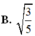
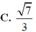
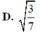
Chọn D
Mặt cầu (S) có tâm I(1;-2;1), bán kính R = 3
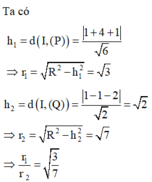
Trong không gian Oxyz, cho mặt phẳng (P): 2x + y + 2z + 2 =0 và cho mặt cầu ( S ) : ( x - 2 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 10 Bán kính của đường tròn giao tuyến giữa (P) và (S) là
A. 7
B. 10
C. 3
D. 1
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): 2x+2y-2z+15=0 và mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 y - 2 z - 1 = 0 Khoảng cách nhỏ nhất từ một điểm thuộc mặt phẳng (P) đến một điểm thuộc mặt cầu (S) là
A. 3 3 2
B. 3
C. 3 2
D. 3 3
Cho mặt cầu ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 và mặt phẳng ( α ): 2x+y-2z+m=0. Các giá trị của m để ( α ) và (S) không có điểm chung là:
A. m ≤ - 9 hoặc m ≥ 21
B. m < - 9 hoặc m > 21
C. - 9 ≤ m ≤ 21
D. - 9 < m < 21
Giúp mình với: trong không gian với hệ toạ độ Oxyz, cho A(1;0;1) và B(-1;1;0) , mặt phăng (P): x+y-2z-5=0 và mặt cầu (S): x^2+y^2+z^2-2x+2y-2z-6=0. viết phương trình mặt phẳng (Q) vuông góc với mp (P), song song với AB và tiếp xúc với mặt cầu (S)
Trong không gian Oxyz , cho mặt cầu
( S ) : ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 25 và mặt phẳng
( P ) : x - 2 y + 2 z + 8 = 0 . Biết (S) cắt (P) theo giao tuyến là một đường tròn có bán kính bằng
A. 3
B. 4
C. 1
D. 2