Vật sáng AB đặt trước thấu kính hội tụ, cho ảnh A ' B ' = A B 2 . Khoảng cách giữa AB và A’B’ là 180cm. Tiêu cự của thấu kính là
A. f = 36cm.
B. f = 40cm.
C. f = 30cm.
D. f = 45cm.
Cho một vật sáng AB cao 5cm đặt trước thấu kính hội tụ có tiêu cự là 25cm, A nằm trên trục chính AB cách thấu kính hội tụ một khoảng d bằng 10cm
a. Dựng ảnh A'B' của vật AB qua thấu kính và cho biết đây là ảnh ảo hay ảnh thật?
b Sau đó dựa vào hình vẽ ,hãy tính khoảng cách từ ảnh tới thấu kính và chiều cao của ảnh
Một vật sáng AB đặt trước thấu kính hội tụ có tiêu cự f, vuông góc với trục chính của thấu kính hội tụ, điểm A nằm trên trục chính. Vật sáng AB qua thấu kính cho ảnh thật A'B'. Chứng minh rằng
A. G = 25.f
B. G = 25 f
C. G = f 25
D. G = 25 - f
Đáp án: B
Giữa độ bội giác và tiêu cự f (đo bằng cm) có hệ thức: 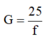
Vật sáng AB có độ cao h= 2 cm, được đặt vuông góc trước một thấu kính hội tụ có tiêu cự d. Điểm A cách thấu kính một khoảng d=2f. Cho biết tiêu cự của thấu kính f=2cm A. Dựng ảnh A'B'của AB tạo bởi thấu kính hội tụ B. Tính chiều cao h'của ảnh và khoảng cách d'từ ảnh tới quang tâm.
Vẽ ảnh của vật sáng AB đặt trước thấu kính =8cm, tiêu cự =12cm
a) Dựng ảnh của vật qua thấu kính hội tụ và thấu kính phân kì
b) Cho h= 1cm .Tính d' và h' ?
Đây là thấu kính hội tụ.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\Rightarrow d'=4,8cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{8}{4,8}\Rightarrow h'=0,6cm\)
đặt vật ab trước một thấu kính hội tụ có tiêu cự f=50cm.Vật AB cách thấu kính khoảng d=60cm.A nằm trên trục chinh,biết vật AB=600mm.a.Dùng các tia sáng đặc biệt qua thấu kính hội tụ về ảnh A'B' của vật AB theo đúng tỉ lệ và nêu tính chất ảnh b.Dùng kiến thức hình học hãy tính khoảng cách từ ảnh đến quang tâm O và độ cao của ảnh A'B'
Một thấu kính hội tụ có tiêu cự f=20cm đặt 1 vật sáng AB trước thấu kính cách thấu kính 1 đoạn bằng 45cm a, tính độ tụ của thấu kính b, tính khoảng cách từ ảnh đến thấu kính
Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính:
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm
Vật sáng AB cao 5cm đặt trước Thấu Kính có tiêu cự 15cm. Vật cách thấu kính 10cm. Hãy dựng ảnh A'B' của AB trong trường hợp a) thấu kính là ,hội tụ b) thấu kính là phân kì
Một vật sáng AB cao 0,5 cm đặt cách thấu kính hội tụ 2 cm Thấu kính có tiêu cự 1,5 cm A. vẽ ảnh A' B' của vật sáng AB B. Tính khoảng cách từ ảnh của vật đến thấu kính
Một thấu kính hội tụ có tiêu cực f=12cm , vật sáng AB đặt trước thấu kính có ảnh A'B'. Tìm vị trí của vật và ảnh biết khoảng cách vật và ảnh là a)125cm b)45cm
Công thức tính thấu kính: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{12d}{d-12}\left(1\right)\)
Gọi khoảng cách từ vật tới ảnh là \(L\): \(\Rightarrow\) \(\left|d+d'\right|=L\)
Vật là vật thật \(\Rightarrow d>0\)
a) Ta có: \(L=125\left(cm\right)\)
TH1: A'B' là ảnh thật ⇒ \(d'>0\)
\(\Rightarrow L=d'+d=125\left(cm\right)\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{12d}{d-12}+d-125=0\Rightarrow d^2-125d+1500=0\)
Giải phương trình lấy nghiệm \(d_1>0\) ta được: \(d_1=111,55cm\) hoặc \(d_1=13,44cm\)
TH2: A'B' là ảnh ảo
\(d'+d=-125cm\left(3\right)\)
Từ (1) và (3) \(\Rightarrow\dfrac{12d}{d-12}+d+125=0\Rightarrow d^2+125d-1500=0\)
Giải phương trình lấy nghiệm \(d>0\) ta được: \(d_1=11\left(cm\right)\)
b) Ta có: \(L=45\left(cm\right)\)
TH1: A'B' là ảnh thật ⇒ \(d>0\)
\(\Rightarrow L=d'+d=45\left(cm\right)\left(4\right)\)
Từ (1) và (4) \(\Rightarrow\dfrac{12d}{d-12}+d-45=0\Leftrightarrow d^2-45d+540=0\)
Phương trình vô nghiệm
TH2: A'B' là ảnh ảo
\(d'+d=-45\left(cm\right)\left(5\right)\)
Từ (1) và (5) \(\Rightarrow\dfrac{12d}{d-12}+d+45\Leftrightarrow d^2+45d-540=0\)
Giải phương trình lấy nghiệm \(d_2>0\) ta được: \(d_2=9,85\left(cm\right)\)