Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, BC = 2a, A B C ⏞ = 60 ° Gọi M là trung điểm của BC. Biết SA=SB=SM= a 39 3 Tìm khoảng cách d từ S đến mặt phẳng (ABC)
A. d = 3a
B. d = a
C. d = 2 a
D. d = 4 a
Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, B C = 2 a , A B C ⏞ = 60 ° . Gọi M là trung điểm của BC Biết SA=SB=SM= a 39 3 Khoảng cách từ S đến mặt phẳng (ABC)
A. 2a
B. 4a
C. 3a
D. a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, B C = 2 a , A B C = 60 ° . Gọi M là trung điểm BC. Biết S A = S B = S M = a 39 3 . Khoảng cách từ điểm S đến mặt phẳng A B C là
A. 2a
B. 3a
C. 4a
D. a
Đáp án A
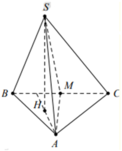
Tam giác ABM có A M = B M A B C ⏜ = 60 ° ⇒ Δ A B M đều cạnh a
Gọi H là tâm đường tròn ngoại tiếp Δ A B M
Mà S A = S B = S M ⇒ H là hình chiếu của S trên m p A B M
Tam giác SAH vuông tại H, có A H = a 3 3 ; S A = a 39 3
Suy ra S H = S A 2 − A H 2 = a 39 3 2 − a 3 3 2 = 2 a
Vậy d S ; ( A B C = S H = 2 a
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, BC=2a, A B C ^ = 60 ° . Gọi M là trung điểm của BC, SA=SC=SM= a 5 . Tính khoảng cách từ điểm S tới mặt phẳng (ABC).
A. a
B. 2a
C. 3a
D. 5a
Cho hình chóp S.ABC có đáy là tam giác vuông tại A , A C = a , B C = 2 a . Hình chiếu của S trên ( ABC) là trung điểm H của BC. Cạnh bên SB tạo với đáy một góc 60 ° . Thể tích khối chóp S.ABC là
A. a 3 6
B. a 3 3 12
C. a 3 3 5
D. a 3 2
Đáp án D
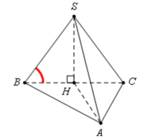
Ta có S H ⊥ A B C ⇒ S B ; A B C ^ = S B ; B C ^ = S B C ^ = 60 °
Tam giác SBH vuông tại H, có S H = tan 60 ° . B H = a 3
Và S A B C = 1 2 . A B . A C = a 2 3 2 .
Vậy thể tích khối chóp là V S . A B C D = 1 3 . S H . S A B C = 1 3 a 3 a 2 3 2 = a 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, BC=2a, ABC=
60
o
Gọi M là trung điểm BC. Biết 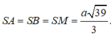 Khoảng cách từ điểm S đến mặt phẳng (ABC) là
Khoảng cách từ điểm S đến mặt phẳng (ABC) là
A. 2a
B. 3a
C. 4a
D. a
Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, BC = 2a, A B C ^ = 60 0 . Gọi M là trung điểm của BC. Biết SA = SM = SB = a 39 3 Khoảng cách từ S đến mặt phẳng (ABC)
A. 2a
B. 4a
C. 3a
D. a
Đáp án A
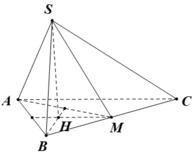
∆ AMB là tam giác đều cạnh a (vì AM = MB = a và A B M ^ = 60 0 )
Gọi H là chân đường cao hạ từ S xuống (ABC). Do SA = SB = SM nên H trùng với trọng tâm tam giác AMB.
Ta có 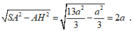
Vậy SH = 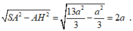
Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, BC = 2a, A B C ^ = 60 0 . Gọi M là trung điểm của BC. Biết SA = SB = SM = a 39 3 . Tìm khoảng cách d từ S đến mặt phẳng (ABC)
A. d = 3a
B. d = a
C. d = 2a
D. d = 4a
Đáp án C
Ta có M là trung điểm của BC nên
Suy ra tam giác ABM là tam giác đều. Gọi H là hình chiếu vuông góc của S xuốn (ABM).
Suy ra H là tâm đường tròn ngoại tiếp tam giác ABM
![]()
Khi đó ![]()
![]()
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, BC=2a; A B C ⏜ = 60 0 . Gọi M là trung điểm của BC, SA=SC=SM= a 5 . Tính khoảng cách từ điểm S tới mặt phẳng (ABC).
A. a
B. 2a
C. a 3
D. a 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=2a và B C = 2 a 3 . Gọi M là trung điểm của BC, hình chiếu vuông góc của S xuống mặt phẳng đáy là điểm nằm trên AM thỏa mãn A H → = 2 H M → . Góc giữa hai mặt phẳng (SAB) và (ABC) bằng 45 ° . Thể tích khối chóp S.ABC là
A. 8 a 3 3 3
B. 8 a 3 3 9
C. 8 a 3 3
D. 8 a 3 9