Đáp án C
Ta có M là trung điểm của BC nên
Suy ra tam giác ABM là tam giác đều. Gọi H là hình chiếu vuông góc của S xuốn (ABM).
Suy ra H là tâm đường tròn ngoại tiếp tam giác ABM
Khi đó 
Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, BC = 2a, A B C ^ = 60 0 . Gọi M là trung điểm của BC. Biết SA = SM = SB = a 39 3 Khoảng cách từ S đến mặt phẳng (ABC)
A. 2a
B. 4a
C. 3a
D. a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 3a, BC = 4a, mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB = 2a 3 và S B C ^ = 30 0 . Tính khoảng cách từ B đến mặt phẳng (SAC) theo a.
A . 3 a 5
B . a 7
C . 6 a 7
D . 3 a 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại đỉnh B với AC =2a, BC =a. Đỉnh S cách đều các điểm A, B, C. Biết góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 o Khoảng cách từ trung điểm M của SC đến mặt phẳng (SAB) bằng
A. a 39 13
B. 3 a 13 13
C. a 39 26
D. a 13 26
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, BC=2a, ABC=
60
o
Gọi M là trung điểm BC. Biết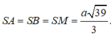 
Khoảng cách từ điểm S đến mặt phẳng (ABC) là
A. 2a
B. 3a
C. 4a
D. a
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60 o . Gọi M là trung điểm của cạnh AB. Tính khoảng cách d từ B đến mặt phẳng (SMC).
A. d = a 39 13
B. d = a 2
C. d = a
D. d = a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, cạnh bên SA vuông góc với đáy và SA = a 2 . Gọi M là trung điểm của AB. Tính khoảng cách d giữa hai đường thẳng SM và BC
A . d = a 3 2
B . d = a 2 3
C . d = a 3 3
D . d = a 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB= 3a, BC = 4a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC và đáy bằng 60 o . Gọi M là trung điểm của AC, tính khoảng cách d giữa hai đường thẳng AB và SM.
A. d = a 3
B. d = 5 a 3
C. d = 5 a 2
D. d = 10 a 3 79
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy.
a) Chứng minh tam giác SBC vuông
b) Gọi H là chân đường cao vẽ từ B của tam giác ABC.
Chứng minh (SAC) ⊥ (SBH)
c) Cho AB = a, BC = 2a. Tính khoảng cách từ B đến mặt phẳng (SAC)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA ⊥ (ABC), SA= 3a, AB=a 2 , BC=2a. Gọi E là trung điểm BC. Tính góc giữa đường thẳng SE và mặt phẳng (ABC)
A. 60 o .
B. 45 o .
C. 30 o .
D. 55 o .
