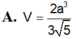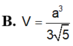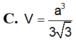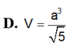Cho khối chóp tam giác SABC có AB=AC=a, ∠ B A C = 120 ° , ∠ S B A = S C A = 90 ° . Góc giữa SB và mặt phẳng (ABC) bằng 60 ° . Thể tích khối chóp S.ABC bằng
A. a 3 4
B. 3 a 3 4
C. a 3 2
D. 3 a 3 2
Những câu hỏi liên quan
Cho hình chóp SABC có tam giác ABC vuông tại A, AB=AC=a. I là trung điểm của SC.Hình chiếu vuông góc của S lên mp (ABC) là trung điểm H của BC , mp (SAB) tạo với đáy một góc 60. Tính thể tích khối chóp SABC và khoảng cách từ I tới mp (SAB) theo a
chứng minh được AH=BH -> SA= SB _> tam giác SAB cân ở S
gọi M là trung điểm của AB -> SM vuông góc với AB -> góc giữa mp (SAB) và mp (ABC) là góc SMH -> góc SMH = 60 độ
-> tìm được SH -> tìm được thể tích
tìm diên tích tam giác SAB -> khoảng cách từ C đến mp (SAB)
Vì I là trung điểm của SC nên khoảng cách từ I đến mp (SAB) bằng một nửa khoảng cách từ C đến mp (SAB)
Đúng 0
Bình luận (0)
Cho hình chóp SABC có đáy là tam giác ABC vuông tại B. SA vuông góc với(ABC), AB = a, AC = 3a, SA = 2a.
a. chứng minh BC vuông góc (ABC).
b. Tính thể tích khối chóp SABC.
Cho hình chóp SABC có các cạnh bên nghiêng đều trên đáy một góc 60 độ. Biết tam giác ABC có AB=a, AC=2a, BC=5a/2. Tính thể tích khối chóp SABC
Gọi H là hình chiếu vuông góc của S lên đáy
\(\Rightarrow\widehat{SAH}=\widehat{SBH}=\widehat{SCH}=60^0\)
\(\Rightarrow AH=BH=CH=\dfrac{SH}{tan60^0}\Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác đáy
\(\Rightarrow AH=R=\dfrac{AB.BC.AC}{4S_{ABC}}\)
\(\Rightarrow SH=AH.tan60^0=\dfrac{AB.BC.AC.\sqrt{3}}{4S_{ABC}}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{AB.BC.CA.\sqrt{3}}{4S_{ABC}}.S_{ABC}=\dfrac{5a^3\sqrt{3}}{12}\)
Đúng 1
Bình luận (0)
Cho hình chóp SABD có tam giác ABC vuông tại A, AB2a, AC3a, SA vuông góc với đáy và SAa. Thể tích khối chóp SABC bằng A.
2
a
3
B.
6
a
3
C.
3
a
3
D.
a
3
Đọc tiếp
Cho hình chóp SABD có tam giác ABC vuông tại A, AB=2a, AC=3a, SA vuông góc với đáy và SA=a. Thể tích khối chóp SABC bằng
A. 2 a 3
B. 6 a 3
C. 3 a 3
D. a 3
cho hình chóp sabc có sa=sb=sc=2a, tam giác vuông tại a có ab=a/2, bc=a. tính thể tích khối chóp sabc
\(AC=\sqrt{BC^2-AB^2}=\dfrac{a\sqrt{3}}{4}\)
Gọi H là hình chiếu vuông góc của S lên đáy
Do \(SA=SB=SC\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đường tròn ngoại tiếp ABC
Mà ABC vuông tại A \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow BH=\dfrac{1}{2}BC=\dfrac{a}{2}\)
\(\Rightarrow SH=\sqrt{SB^2-BH^2}=\dfrac{a\sqrt{15}}{2}\)
\(V=\dfrac{1}{3}SH.\dfrac{1}{2}AB.AC=\dfrac{1}{3}.\dfrac{a\sqrt{15}}{2}.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{4}=\dfrac{a^3\sqrt{5}}{32}\)
Đúng 0
Bình luận (0)
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, cạnh AB 2,
A
B
C
^
60
°
. Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm M của BC, góc giữa SA và mặt đáy bằng 450. Thể tích của khối chóp SABC bằng
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, A B C ^ = 60 ° . Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm M của BC, góc giữa SA và mặt đáy bằng 450. Thể tích của khối chóp SABC bằng
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, cạnh AB 2,
A
B
C
^
60
°
. Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm M của BC, góc giữa SA và mặt đáy bằng
45
°
. Thể tích của khối chóp SABC bằng A.
4
3
3...
Đọc tiếp
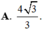
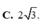
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, A B C ^ = 60 ° . Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm M của BC, góc giữa SA và mặt đáy bằng 45 ° . Thể tích của khối chóp SABC bằng
A. 4 3 3
B. 4 3
C. 2 3
D. 2
15 tháng 6 2021 lúc 21:08
cho hình chóp SABC có tam giác ABC vuông cân tại A, AB=a, tam giác SAB cân tại S. (SAB) vuông góc với (ABC). (SBC) tạo với đáy 1 góc 45°. Tính thể tích SABC
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành thỏa mãn ABa, ACa
3
. Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng (SBC) bằng
a
3
3
. Tính thể tích V của khối chóp đã cho
Đọc tiếp
Cho hình chóp .S ABCD có đáy ABCD là hình bình hành thỏa mãn AB=a, AC=a 3 . Biết tam giác SBC cân tại S, tam giác SCD vuông tại C và khoảng cách từ D đến mặt phẳng (SBC) bằng a 3 3 . Tính thể tích V của khối chóp đã cho
