Trong không gian Oxyz cho a → , b → tạo với nhau 1 góc 120 ° và a → = 3 ; b → = 5. Tìm T = a → − b → .
A. 5
B. 6
C. 7
D. 4
Trong không gian Oxyz cho a → , b → tạo với nhau 1 góc 120 o và a → = 3 , b → = 5 . Tìm T = a → - b →
A. T = 5
B. T = 6
C. T = 7
D. T = 4
Trong không gian với hệ tọa độ Oxyz, cho vecto a → 1 ; - 2 ; 4 và b → x 0 ; y 0 ; z 0 cùng phương với vectơ a → . Biết vectơ b → tạo với tia Oy một góc nhọn và b → = 21 . Tính tổng x 0 + y 0 + z 0
A. x 0 + y 0 + z 0 = 3
B. x 0 + y 0 + z 0 = -3
C. x 0 + y 0 + z 0 = 6
D. x 0 + y 0 + z 0 = -6
Do b → x 0 ; y 0 ; z 0 cùng phương với a → 1 ; - 2 ; 4 nên b → k ; - 2 k ; 4 k
Mà b → = 21 = k 2 + 4 k 2 + 16 k 2 = 21 k 2 nên suy ra
Do đó x 0 = - 1 ; y 0 = 2 ; z 0 = - 4
Vậy x 0 + y 0 + z 0 = -3
Đáp án B
Trong không gian tọa độ Oxyz, cho A(1;3;10), B(4;6;5) và M là điểm thay đổi trên mặt phẳng (Oxy) sao cho MA, MB cùng tạo với mặt phẳng (Oxy) các góc bằng nhau. Tìm giá trị nhỏ nhất của AM
A. 6 3 6
B. 10
C. 10
D. 8 2
Trong không gian với hệ tọa độ Oxyz, cho vecto a → = 1 ; − 2 ; 4 v à b → = x 0 ; y 0 ; z 0 cùng phương với vecto a → . Biết vecto b → tạo với tia Oy một góc nhọn và b → = 21 . Khi đó tổng x 0 + y 0 + z 0 bằng bao nhiêu?
A. x 0 + y 0 + z 0 = 3.
B. x 0 + y 0 + z 0 = − 3.
C. x 0 + y 0 + z 0 = 6.
D. x 0 + y 0 + z 0 = − 6.
Trong không gian với hệ tọa Oxyz, cho vectơ a → = 1 ; - 2 ; 4 , b → = x 0 ; y 0 ; z 0 cùng phương với vectơ a → . Biết vectơ b → tạo với tia Oy một góc nhọn và b → = 21 . Giá trị của tổng x 0 + y 0 + z 0 bằng
A. - 3
B. 6
C. - 6
D. 3
Trong không gian với hệ tọa Oxyz, cho vectơ a → = ( 1 ; - 2 ; 4 ) , b → = x 0 ; y 0 ; z 0 cùng phương với vectơ a → . Biết vectơ b → tạo với tia Oy một góc nhọn và b → = 21 . Giá trị của tổng x 0 + y 0 + z 0 bằng
A. -3
B. 6
C. -6
D. 3
Chọn A
Do a → , b → cùng phương và nên b → =k a → (k ≠ 0) ta có
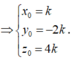
Suy ra
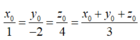
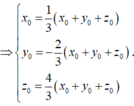
Theo giả thiết vectơ b → tạo với tia Oy một góc nhọn nên
![]()
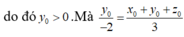
![]()
![]()
suy ra
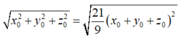
![]()
![]()
Trong không gian Oxyz, véctơ u → vuông góc với hai véctơ a → = 1 ; 1 ; 1 và b → = 1 ; - 1 ; 3 ; đồng thời u → tạo với tia Oz một góc tù và độ dài véctơ u → bằng 3. Tìm véctơ u → .
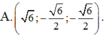
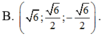
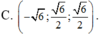
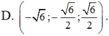
Trong không gian Oxyz, cho hai điểm A(-1;1;2), B(1;2;-1) Phương trình mặt phẳng chứa đường thẳng AB và tạo với mặt phẳng α : x + 2 y - 2 z + 3 = 0 một góc nhỏ nhất là
A. x+4y+2z-7=0
B. x+y+z-2=0
C. x-5y-3z+12=0
D. 3x-9y-z+14=0
Có
A
B
⇀
(
2
;
1
;
-
3
)
và
n
α
⇀
(
1
;
2
;
-
2
)
Gọi
n
⇀
(
a
,
b
,
c
)
là véctơ pháp tuyến của mặt phẳng cần tìm, ta có ![]()
![]()
Góc giữa hai mặt phẳng xác định bởi:
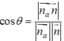
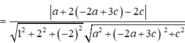
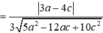
Đặt ![]() khi đó
khi đó
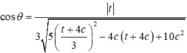
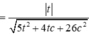
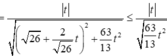
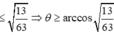
Dấu bằng đạt tại 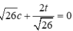
![]()
Do đó (P): 3x-9y-z+14=0
Chọn đáp án D.
*Chú ý câu hỏi này các em nên thử đáp án cho nhanh.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 4 x - 7 y + z + 25 = 0 và đường thẳng d 1 : x + 1 1 = y 2 = z - 1 - 1 . Gọi d 1 ' là hình chiếu vuông góc của d 1 lên mặt phẳng P . Đường thẳng d 2 nằm trên P tạo với d 1 , d 1 ' các góc bằng nhau, d 2 có vectơ chỉ phương u 2 → = a ; b ; c . Tính a + 2 b c
A. a + 2 b c = 2 3
B. a + 2 b c = 0
C. a + 2 b c = 1 3
D. a + 2 b c = 1