Có bao nhiêu giá trị nguyên của mÎ[0;2018] để bất phương trình m + e π 2 ≥ e 2 x + 1 4 có nghiệm với mọi xÎR
A. 2016
B. 2017
C. 2018
D. 2019
Có bao nhiêu giá trị nguyên của tham số mÎ[-10;10] để bất phương trình sau nghiệm đúng ∀ x ∈ R : 6 + 2 7 x + 2 - m 3 - 7 x - m + 1 2 x ≥ 0
A. 10
B. 9
C. 12
D. 11
Có bao nhiêu giá trị nguyên của tham số mÎ(−2018;2018) để hàm số y = 2 x - 6 x - m đồng biến trên khoảng (5;+¥) ?
A. 2018 .
B. 2021.
C. 2019 .
D. 2020 .
Có bao nhiêu giá trị nguyên của tham số mÎ[-2018;2019] để đồ thị hàm số y = x 3 - 3 m x + 3 và đường thẳng y = 3 x + 1 có duy nhất một điểm chung?
A. 1
B. 2019
C. 4038
D. 2018
Chọn đáp án D
Phương pháp
Đồ thị hàm số y=f(x) và đường thẳng y=g(x) có duy nhất 1 điểm chung ⇒ phương trình hoành độ giao điểm f(x)=g(x) có nghiệm duy nhất.
Cách giải
Phương trình hoành độ giao điểm của đồ thị hai đồ thị hàm số là
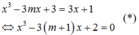
Hai đồ thị hàm số có duy nhất 1 điểm chung khi và chỉ khi phương trình (*) có nghiệm duy nhất

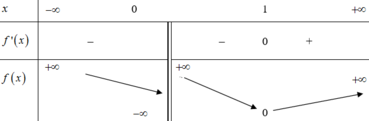

Số giá trị nguyên của tham số mÎ[-10;10] để bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 nghiệm đúng ∀ x ∈ [ - 3 ; 6 ] là
A. 28
B. 20
C. 4
D. 19
Cho A = 2 x - 1 x + 2 với x ≥ 0. Có bao nhiêu giá trị của x để A có giá trị nguyên.
A. 2
B. 1
C. 0
D. 3
Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình log 2 2 x + m log 2 x - m ≥ 0 nghiệm đúng với mọi giá trị của x ∈ 0 ; + ∞ ?
A. Có 4 giá trị nguyên
B. Có 6 giá trị nguyên
C. Có 5 giá trị nguyên
D. Có 7 giá trị nguyên
Đáp án C
Đặt t = log 2 x với x ∈ 0 ; + ∞ thì t ∈ ℝ , khi đó bất phương trình trở thành t 2 + m t - m > 0 *
Để (*) nghiệm đúng với mọi t ∈ ℝ ⇔ ∆ * ≤ 0 ⇔ m 2 + 4 m ≤ 0 ⇔ m ∈ - 4 ; 0
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện
Có bao nhiêu giá trị nguyên của a để phương trình cos 3 2 x − cos 2 2 x − a sin 2 x = 0 có nghiệm thuộc khoảng 0 ; π 6 .
A. 0
B. 1
C. 2
D. 3
Có bao nhiêu giá trị nguyên của m để phương trình cos2x-4cosx-m= 0 có nghiệm
A. 6
B. 7
C. 9
D. 8
Có bao nhiêu giá trị nguyên của m để phương trình cos 2 x − 4 cos x − m = 0 có nghiệm.
A. 6
B. 7
C. 8
D. 9
Đáp án D
Ta có: P T ⇔ 2 cos 2 x − 1 − 4 cos x = m
→ t − cos x f t = 2 t 2 − 4 t − 1 = m t ∈ − 1 ; 1
Khi đó: f ' t = 4 t − 4 = 0 ⇔ t = 1
Lại có: f 1 = 5 ; f 1 = − 3 do đó PT đã cho có nghiệm
⇔ m ∈ − 3 ; 5 ⇒ có 9 giá trị nguyên của m