Cho khối tứ diện ABCD có B C = 3 , C D = 4 , A B C ^ = B C D ^ = A D C ^ = 90 ° Góc giữa hai đường thẳng AD và BC bằng 60 ° Côsin góc giữa hai mặt phẳng (ABC) và (ACD) bằng
A. 2 43 43
B. 43 86
C. 4 43 43
D. 43 43
Những câu hỏi liên quan
Cho tứ diện ABCD. Gọi B' và C' lần lượt là trung điểm của AB và AC. Tỉ số thể tích của khối tứ diện AB'C'D và khối tứ diện ABCD bằng:
A. 1/2 B. 1/4
C. 1/6 D. 1/8.
Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành 4 khối tứ diện:
A. AMCN, AMND, BMCN, BMND
B. AMCN, AMND, AMCD, BMCN
C. BMCD, BMND, AMCN, AMDN
D. AMCD, AMND, BMCN, BMND.
Chọn A.
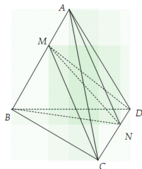
Nhìn vào hình vẽ ta thấy MN là giao tuyến của hai mặt phẳng (MCD) và (NAB), khi đó ta thấy tứ diện đã cho được chia thành bốn tứ diện ACMN, AMND, BMNC, BMND.
Đúng 0
Bình luận (0)
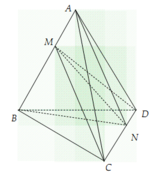
Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành 4 khối tứ diện:
A. AMCN, AMND, BMCN, BMND
B. AMCN, AMND, AMCD, BMCN
C. BMCD, BMND, AMCN, AMDN
D. AMCD, AMND, BMCN, BMND
Chọn A.
Nhìn vào hình vẽ ta thấy MN là giao tuyến của hai mặt phẳng (MCD) và (NAB), khi đó ta thấy tứ diện đã cho được chia thành bốn tứ diện ACMN,AMND,BMNC,BMND.
Đúng 0
Bình luận (0)
trong hệ trục tọa độ oxyz cho 4 điểm A(1;-2;0), B(2;0;3), C(-2;1;3) và D(0;1;1) thể tích khối tứ diện ABCD bằng A.6 B.8 C.12 D.4
\(\overrightarrow{AB}=\left(1;2;3\right)\) ; \(\overrightarrow{AC}=\left(-3;3;3\right)\) ; \(\overrightarrow{AD}=\left(-1;3;1\right)\)
\(V_{ABCD}=\dfrac{1}{6}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right].\overrightarrow{AD}\right|=4\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B, C, D sao cho thể tích của khối tứ diện ABCD nhỏ nhất và
A
B
A
B
+
A
C
A
C
+
A...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B', C', D' sao cho thể tích của khối tứ diện AB'C'D' nhỏ nhất và A B A B ' + A C A C ' + A D A D ' = 4 . Tìm phương trình của mặt phẳng (B’C’D’)
A. 16 x + 40 y - 44 z + 39 = 0
B. 16 x - 40 y - 44 z + 39 = 0
C. 16 x + 40 y + 44 z + 39 = 0
D. 16 x + 40 y - 44 z - 39 = 0
Cho tứ diện ABCD có
A
B
,
A
C
,
A
D
đôi một vuông góc với nhau,
A
B
a
,
A
C
b
,
A
D
c
.
Tính thể tích V của khối tứ diện ABCD theo a, b, c A.
V
a
b
c
2...
Đọc tiếp
Cho tứ diện ABCD có A B , A C , A D đôi một vuông góc với nhau, A B = a , A C = b , A D = c . Tính thể tích V của khối tứ diện ABCD theo a, b, c
A. V = a b c 2
B. V = a b c 6
C. V = a b c 3
D. V = a b c
Đáp án B
V A . B C D = 1 3 A D . S A B C = 1 6 A B . A C . A D = a b c 6
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, ABa, ACb, ADc Tính thể tích V của khối tứ diện ABCD theo a, b, c
Đọc tiếp
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, AB=a, AC=b, AD=c Tính thể tích V của khối tứ diện ABCD theo a, b, c
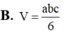
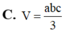
Cho tứ diện ABCD có thể tích là V. Gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Tính thể tích khối tứ diện A'B'C'D' theo V.
Cho tứ diện đều ABCD có cạnh a. Lấy các điểm B',C' trên AB và AC sao cho AB'=a/2; AC' =2a/3. Tính thể tích khối tứ diện AB'C'D
Trong không gian Oxyz, cho tứ diện ABCD với A(-1;-2;4), B(-4;-2;0), C(3;-2;1), D(1;1;1). Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D bằng
A. 3
B. 1
C. 2
D. 1 2
