Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y = - x 4 + 2 m x 2 - 2 m có 3 điểm cực trị tạo tam giác có diện tích bằng 1
A. m = 3
B. m = 1 4 5
C. m = 1
D. m = - 1
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y = x − 1 + 2017 x 2 − 2 m x + m + 2 đúng 3 đường tiệm cận?
A. 2 < m ≤ 3
B. 2 ≤ m ≤ 3
C. m < 2
D. m > 2 hoặc m < − 1
Đáp án A
Ta có: lim x → + ∞ y = 0 ⇒ đồ thị hàm số có 1 tiệm cận ngang là y = 0 .
Để đồ thị hàm số có 3 tiệm cận thì phương trình : g x = x 2 − 2 m x + m + 2 = 0 có 2 nghiệm phân biệt
x 1 > x 2 ⇔ Δ ' = m 2 − m − 2 > 0 x 1 − 1 x 2 − 1 ≥ 0 x 1 − 1 + x 2 − 1 > 0 ⇔ m + 1 m − 2 > 0 x 1 x 2 − x 1 + x 2 + 1 ≥ 0 x 2 + x 2 > 2 ⇔ m + 1 m − 2 > 0 m + 2 − 2 m + 1 > 0 2 m > 2 ⇔ 3 ≥ m > 2.
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{x^2-mx-2m^2}{x-2}\) có tiệm cận đứng .
Hàm có tiệm cận đứng khi và chỉ khi \(x^2-mx-2m^2=0\) vô nghiệm hoặc không có nghiệm \(x=2\)
\(\Rightarrow\left[{}\begin{matrix}\Delta=m^2+8m^2< 0\\4-2m-2m^2\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne1\\m\ne-2\end{matrix}\right.\)
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{x+1}{\sqrt{mx^2+1}}\) có 2 tiệm cận ngang.
Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{5x-3}{x^2-2mx+1}\) không có tiệm cận đứng .
Do mẫu có bậc 2 còn tử bậc 1 \(\Rightarrow\)hàm không có tiệm cận đứng khi và chỉ khi phương trình \(x^2-2mx+1=0\) vô nghiệm
\(\Leftrightarrow\Delta'=m^2-1< 0\)
\(\Rightarrow-1< m< 1\)
cho hàm số y=2mx+m+2 (m là tham số)
tìm tất cả các giá trị của m để đồ thị hàm số đó song song với đường thẳng y=(m^2-3)x+2m-1
Trả lời :
Bn Do Phuong Mai đừng bình luận linh tinh nhé !
- Hok tốt !
^_^
tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số \(y=\dfrac{\sqrt{1-x}}{x-m}\) có tiệm cận đứng .
ĐKXĐ: \(x\le1\)
Hàm có tiệm cận đứng khi và chỉ khi phương trình:
\(x-m=0\) có nghiệm \(x< 1\)
\(\Leftrightarrow m< 1\)
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = x 2 - x - m + 1 x - m không có tiệm cận đứng.
A. m = 1
B. m = ± 1
C. m = -1
D. m ≠ 1
Đáp án A.
Đồ thị hàm số không có tiệm cận đứng
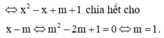
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x + 1 m 2 x 2 − m − 2 có bốn đường tiệm cận.
A. m ≠ 0 m < − 2
B. m ∉ 0 ; − 1 m ≥ − 2
C. m ∉ 0 ; − 1 ; 2 m > − 2
D. m ≠ 2 m > − 2
Tìm tất cả các giá trị tham số m để hai đồ thị hàm số \(y=-x^2-2x+3\) và \(y=x^2-m\) có điểm chung
Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4