Cho tứ diện đều ABCD. Tính tang của góc giữa AB và (BCD)
A. 3
B. 1 3
C. 2
D. 1 2
Cho tứ diện ABCD có AB ⊥ (BCD) và AB=a√3, BCD là tam giác đều cạnh a.Tính góc giữa: 1) AC và (BCD) 2) AD và (BCD) 3) AD và (ABC)
Cho tứ diện đều ABCD . Tính tan của góc giữa AB và (BCD)
A. 3
B. 1 3
C. 2
D. 1 2
Đáp án C
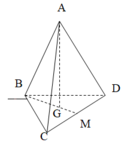
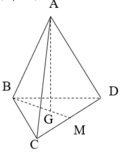
Ta có: BM là hình chiếu vuông góc của AB lên mặt phẳng (BCD)
Cho tứ diện đều ABCD . Tính tan của góc giữa AB và (BCD)
A. 3
B. 1 3
C. 2
D. 1 2
Đáp án C
Ta có: BM là hình chiếu vuông góc của AB lên mặt phẳng (BCD)
⇒ ( A B , ( B C D ) ) = ( A B , B M ) B M = a 3 2 ⇒ B G = a 3 3 A G = a 2 − a 2 3 = a 6 3 ⇒ tan α = A G B G = 2
Cho tứ diện đều ABCD . Tính tan của góc giữa AB và (BCD)
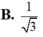
Đáp án C
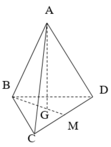
Ta có: BM là hình chiếu vuông góc của AB lên mặt phẳng (BCD)
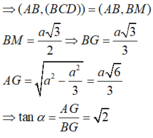
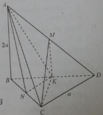
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa CM với mặt phẳng (BCD) bằng:
A. 2 3 3
B. 3 2
C. 2 3
D. không xác định
Cho tứ diện đều ABCD cạnh a. Gọi φ là góc giữa đường thẳng AB và mặt phẳng (BCD). Tính cosφ .
A. cosφ = 3 3
B. cosφ = 2 3
C. cosφ = 1 2
D. cosφ = 3 2
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 O . Tính thể tích V của khối tứ diện ABCD theo a:
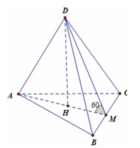
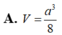
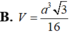
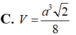
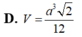
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 ° . Tính thể tích V của khối tứ diện ABCD theo a:
A. V = a 3 8
B. V = a 3 3 16
C. V = a 3 2 8
D. V = a 3 2 12
Đáp án B
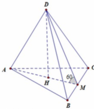
Gọi M là trung điểm của BC khi đó D M ⊥ B C A M ⊥ B C
Suy ra B C ⊥ ( D M A ) ⇒ D B C ; A B C ^ = 60 °
Lại có D M = A M = a 3 2
Dựng D H ⊥ A M ⇒ D H ⊥ ( A B C )
Khi đó V A B C D = 1 3 D H . S A B C = 1 3 D M . sin 60 ° . a 2 3 4 = a 2 3 16 .
