Hàm số nào sau đây không có cực trị?
A. y = x 3 − 3 x 2 + 2007
B. y = 2 x + 1 x − 3
C. y = x 2 + 3 x + 2
Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không.
• y = -2x + 1;
• y = x/3(x-3)2 (H.8).
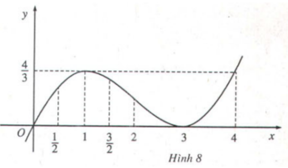
Hàm số y = -2x + 1 không có cực trị.
Hàm số y = x/3 (x-3)2 đạt cực đại tại x = 1 và đạt cực tiểu tại x = 3.
Cho a,b,c∈R sao cho hàm số y=x 3 + ax 2 + bx + c đạt cực trị tại x = 2 đồng thời có y(0)=1 và y(2)=-3. Hỏi trong không gian Oxyz, điểm M(a;b;c) nằm trong mặt cầu nào sau đây?
A. ( x - 1 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 16 .
B. ( x - 2 ) 2 + ( y - 3 ) 2 + ( z + 5 ) 2 = 64 .
C. x 2 + y 2 + ( z + 5 ) 2 = 36 .
D. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 .
Cho a , b , c ∈ R sao cho hàm số y = x 3 + a x 2 + b x + c đạt cực trị tại x = 3, đồng thời có y ( 0 ) = 3 và y 3 = 3 . Hỏi trong không gian Oxyz, điểm M ( a , b , c ) nằm trong mặt cầu nào sau đây?
![]()
![]()
![]()
![]()
Đáp án D.
Từ y(0)=3 và y(3)=3, ta có:
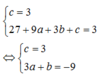
Hàm số đạt cực trị tại x = 3 nên
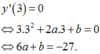
Do đó ![]() Do đó:
Do đó: ![]() nằm trong mặt cầu ở đáp án D.
nằm trong mặt cầu ở đáp án D.
Chú ý: Điểm M nằm trong mặt cầu tâm I bán kính R khi và chỉ khi I M ≤ R
a,Hàm số y = -2x + 1 không có cực trị.
Hàm số y = x/3 (x-3)2 đạt cực đại tại x = 1 và đạt cực tiểu tại x = 3.
a. Hàm số y = -2x + 1 có đồ thị là đường thẳng => Không có cực trị ( điều này hiển nhiên )
b) \(y=f\left(x\right)=\frac{x}{3}\left(x-3\right)^2\)
Có:
\(y'=f'\left(x\right)=\frac{1}{3}.\left(x-3\right)^2+\frac{x}{3}.2.\left(x-3\right)=\frac{1}{3}\left(x-3\right)\left(x-3+2x\right)=\left(x-3\right)\left(x-1\right)\)
\(f''\left(x\right)=x-1+x-3=2x-4\)
+) \(f'\left(x\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)
+) Với x =3 có: \(f''\left(3\right)=2.3-4=2>0\)=> y = f ( x ) đạt cực tiểu tại x = 3.
+ Với x = 1 có: \(f''\left(1\right)=2.1-4=-1< 0\)=> y = f ( x ) đạt cực đại tại x =1
Còn có nhiều cách khác nữa: Vẽ đồ thị, vẽ bảng biến thiên,...
hay vải chưởng đè sai mà bn vẫn làm được
Cho a , b , c ∈ R sao cho hàm số y = x 3 + a x 2 + b x + c đạt cực trị tại x = 3, đồng thời có y 0 = 3 và y 3 = 3 . Hỏi trong không gian Oxyz, điểm M a ; b ; c nằm trong mặt cầu nào sau đây?
A. x − 2 2 + y − 3 2 + z + 5 2 = 130.
B. x − 1 2 + y − 1 2 + z − 1 2 = 40.
C. x 2 + y 2 + z + 5 2 = 90.
D. x + 5 2 + y − 7 2 + z + 3 2 = 42.
Đáp án D.
Từ y 0 = 3 và y 3 = 3 , ta có:
c = 3 27 + 9 a + 3 b + c = 3 ⇔ c = 3 3 a + b = − 9
Hàm số đạt cực trị tại x = 3 nên
y ' 3 = 0 ⇔ 3.3 2 + 2 a .3 + b = 0 ⇔ 6 a + b = − 27.
Do đó a = − 6 ; b = 9 ; c = 3. Do đó: M − 6 ; 9 ; 3 nằm trong mặt cầu ở đáp án D.
Chú ý: Điểm M nằm trong mặt cầu tâm I bán kính R khi và chỉ khi I M ≤ R .
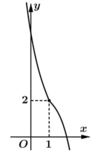
Cho hàm số y = f(x) có đạo hàm trên ℝ và không có cực trị, đồ thị của hàm số y = f(x) là đường cong ở hình vẽ bên. Xét hàm số h x = 1 2 f x 2 - 2 x f x + 2 x 2 . Mệnh đề nào sau đây đúng?
A. Đồ thị hàm số y = h(x) có điểm cực tiểu là M(1;0)
B. Đồ thị hàm số y = h(x) không có cực trị.
C. Đồ thị của hàm số y = h(x) có điềm cực đại là N(1;2)
D. Đồ thị hàm số y = h(x) có điểm cực đại là M(1;0)
Ta có ![]()
Suy ra ![]()
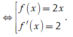
• Từ giả thiết hàm số không có cực trị, kết hợp với đồ thị suy ra hàm số luôn nghịch biến nên f'(x) < 0 với mọi x. Suy ra f'(x) - 2 < 0 với mọi x
• Phương trình f(x) = 2x có nghiệm suy nhất x = 1 (VT nghịch biến – VP đồng biến).
Bảng biến thiên
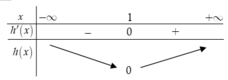
Do đó đồ thị hàm số y = h(x) có điểm cực tiểu M(1;0)
Chọn A.
Cho hàm số y = f(x) có đạo hàm trên M và không có cực trị, đồ thị của hàm số y = f(x) là đường cong ở hình vẽ bên. Xét hàm số h x = 1 2 f x 2 - 2 x f x + 2 x 2 . Mệnh đề nào sau đây đúng?
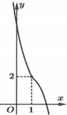
A. Đồ thị hàm số y = h(x) có điểm cực tiểu là M (1;0).
B. Hàm số y = h(x) không có cực trị.
C. Đồ thị của hàm số y = h(x) có điểm cực đại là N(1;2).
D. Đồ thị hàm số y = h(x) có điểm cực đại là M (1;0).
còn ai treen olinemath ko
a,Hàm số y = -2x + 1 không có cực trị.
Hàm số y = x/3 (x-3)2 đạt cực đại tại x = 1 và đạt cực tiểu tại x = 3.
1. Cho hàm số \(y=\dfrac{3x^2+13x+19}{x+3}\). Đường thẳng đi qua 2 điểm cực trị của đths có phương trình là:
\(A.5x-2y+13=0\)
\(B.y=3x+13\)
\(C.y=6x+13\)
\(D.2x+4y-1=0\)
2. Cho hàm số \(y=\sqrt{x^2-2x}\). Khẳng định nào sau đây là đúng?
A. Hàm số có 2 điểm cực trị
B. Hàm số đạt cực tiểu tại x=0
C. Hàm số đại cực đại tại x=2
D. Hàm số có đúng 4 điểm cực trị
3. Cho hàm số \(y=x^7-x^5\). Khẳng định nào sau đây đúng?
A. Hàm số có đúng 1 điểm cực trị
B. Hàm số có đúng 3 điểm cực trị
C. Hàm số có đúng 2 điểm cực trị
D. Hàm số có đúng 4 điểm cực trị
4. Cho hàm số \(y=f\left(x\right)\)có đạo hàm \(f'\left(x\right)=\left(x+1\right)\left(x-2\right)^2\left(x-3\right)^3\left(x+5\right)^4\)
. Hàm số \(y=f\left(x\right)\) có bao nhiêu điểm cực trị?
A. 2
B. 3
C. 4
D. 5
5. Cho hàm số \(y=\left(x^2-2x\right)^{\dfrac{1}{3}}\) . Khẳng định nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x=1
B. Hàm số đạt cực đại tại x=1
C. Hàm số không có điểm cực trị
D. Hàm số có đúng 2 điểm cực trị
Có bao nhiêu mệnh đề đúng trong các phát biểu sau?
1. Hàm số không có đạo hàm tại x = 0.
2. Hàm số không liên tục tại x = 0.
3. Hàm số không có cực trị tại x = 0.
4. Hàm số đạt cực trị tại x = 0.
A. 0
B. 1
C. 2
D. 3
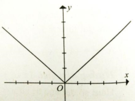
Đồ thị hàm số y = |x| có dạng hình vẽ.
Từ đồ thị trong hình ta có hàm số y = |x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó. Sử dụng định nghĩa cực trị ta có hàm số y = |x| đạt cực tiểu tại x = 0
Do đó mệnh đề 1 và 4 đúng. Chọn đáp án C