Đường cong ở hình dưới là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
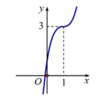
A. y = 2 x 3 - x 2 + 6 x + 1
B. y = 2 x 3 - 6 x 2 + 6 x + 1
C. y = 2 x 3 - 6 x 2 - 6 x + 1
D. y = - 2 x 3 - 6 x 2 - 6 x + 1
Những câu hỏi liên quan
Đường cong ở hình dưới là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A.
2
x
3
-
x
2
+
6
x
+
1
B.
2
x
3
-
6
x
2
+
6
x
+
1
C.
2
x
3
-...
Đọc tiếp
Đường cong ở hình dưới là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
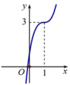
A. 2 x 3 - x 2 + 6 x + 1
B. 2 x 3 - 6 x 2 + 6 x + 1
C. 2 x 3 - 6 x 2 - 6 x + 1
D. - 2 x 3 - 6 x 2 - 6 x + 1
Chọn B.
Ta thấy đồ thị hàm số đi qua điểm I(1;3). Lần lượt thay tọa độ điểm I vào các biểu thức hàm số ở các đáp án, cho ta đáp án B
Đúng 0
Bình luận (0)
Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ? A.
y
x
3
-
3
x
2
+
1
B.
y
-
x
3
+
3
x
2
+
1
C.
y
x
4
+
3...
Đọc tiếp
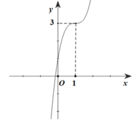
Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ?
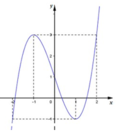
A. y = x 3 - 3 x 2 + 1
B. y = - x 3 + 3 x 2 + 1
C. y = x 4 + 3 x 2 + 1
D. y = x 3 - 3 x + 1
Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ? A.
y
x
3
-
3
x
2
+
1
B.
y
-
x
3
+
3
x
2
+
1
C.
y
x
4
-
2...
Đọc tiếp
Đường cong ở hình bên dưới là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào ?
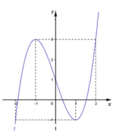
A. y = x 3 - 3 x 2 + 1
B. y = - x 3 + 3 x 2 + 1
C. y = x 4 - 2 x 3 + 1
D. y = x 3 - 3 x + 1
Phương pháp
Dựa vào dáng điệu của đồ thị và các điểm thuộc đồ thị hàm số để đưa ra nhận xét và chọn đáp án đúng.
Cách giải
Ta thấy đồ thị hàm số là hàm bậc 3 có nét cuối đi lên nên hàm số và có a > 0 => loại đáp án B và C.
Đồ thị hàm số đi qua điểm (-1;3) nên ta loại đáp án A.
Chọn D.
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A.
y
−
2
x
3
−
6
x
2
−
6
x
+
1
B.
y
2
x
3
−
6
x
2
+
6
x
+
1
C.
y...
Đọc tiếp
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
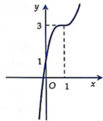
A. y = − 2 x 3 − 6 x 2 − 6 x + 1
B. y = 2 x 3 − 6 x 2 + 6 x + 1
C. y = 2 x 3 − 6 x 2 − 6 x + 1
D. y = 2 x 3 − x 2 + 6 x + 1
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A.
y
−
2
x
3
−
6
x
2
−
6
x
+
1
B.
y
2
x
3
−
6
x
2
+
6
x
+
1
C.
y...
Đọc tiếp
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
A. y = − 2 x 3 − 6 x 2 − 6 x + 1
B. y = 2 x 3 − 6 x 2 + 6 x + 1
C. y = 2 x 3 − 6 x 2 − 6 x + 1
D. y = 2 x 3 − x 2 + 6 x + 1
Đáp án B
Với x = 1 thì y=3 nên ta loại A; C, D chọn B.
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A.
y
−
2
x
3
−
6
x
2
−
6
x
+
1
B.
y
2
x
3
−
6
x...
Đọc tiếp
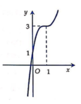
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
A. y = − 2 x 3 − 6 x 2 − 6 x + 1
B. y = 2 x 3 − 6 x 2 + 6 x + 1
C. y = 2 x 3 − 6 x 2 − 6 x + 1
D. y = 2 x 3 − 6 x 2 + 6 x + 1
Đáp án B
Xét hàm số ax3 + bx2+cx+d=0
Do ĐTHS đông biến có chiều hướng lên nên suy ra a > 0 => Loại A
Theo hình vẽ ta thấy ĐTHS qua các điểm (1,3), (0,1)
Thử 3 đáp án suy ra B
Đúng 0
Bình luận (0)
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào? A.
y
-
2
x
3
-
6
x
2
+
6
x...
Đọc tiếp
Đường cong ở hình bên là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?
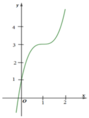
A. y = - 2 x 3 - 6 x 2 + 6 x + 1
B. y = 2 x 3 - 6 x 2 + 6 x + 1
C. y = - 2 x 3 - 6 x 2 - 6 x + 1
D. y = 2 x 3 - 6 x 2 - 6 x + 1
Đáp án B
Phương pháp: Loại trừ phương án sai.
Cách giải: Hàm số ở bốn phương án có dạng 
Quan sát đồ thị hàm số ta thấy hàm số đồng biến trên R => a>0
=> Loại đi phương án A và C.
Mặt khác, hàm số đồng biến trên 
Xét 
y’ = 0 có hai nghiệm phân biệt => 
có khoảng đồng biến, có khoảng nghịch biến.
=>Loại đi phương án D.
=>Chọn phương án B
Đúng 0
Bình luận (0)
Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A.
y
x
4
−
2
x
2
−
1.
B.
y
x
4
−
2
x
2
+
2.
C.
y
x...
Đọc tiếp
Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
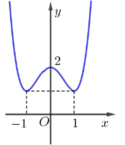
Hỏi hàm số đó là hàm số nào?
A. y = x 4 − 2 x 2 − 1.
B. y = x 4 − 2 x 2 + 2.
C. y = x 4 − 2 x 2 + 1.
D. y = x 4 − 2 x 2 .
Đáp án B
Dựa vào đồ thị hàm số ta có: lim x → + ∞ = + ∞ ⇒ a > 0
Đồ thị hàm số cắt trục Oy tại điểm 0 ; 2 ⇒ d = 2
Đúng 0
Bình luận (0)
Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. y x4 – 2x2 – 1 B. y x4 – 2x2 + 1 C. y x4 – 2x2 D. y x4 – 2x2 + 2
Đọc tiếp
Đường cong trong hình vẽ dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
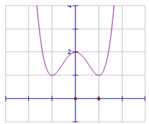
A. y = x4 – 2x2 – 1
B. y = x4 – 2x2 + 1
C. y = x4 – 2x2
D. y = x4 – 2x2 + 2
Đáp án D.
Ta thấy đồ thị hàm số đã cho cắt trục tung tại điểm A(0; 2).
Do đó đồ thị ở đáp án D là đáp án duy nhất thỏa mãn đầu bài
Đúng 0
Bình luận (0)